Вам понадобится
- уравнения прямых
Инструкция
1
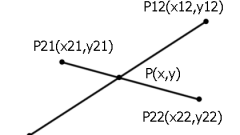
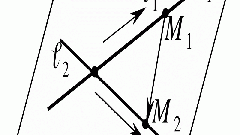
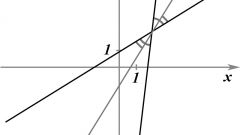
В декартовых координатах общее уравнение прямой выглидит так: Ax+By+C = 0. Пусть две прямые пересекаются. Уравнение первой прямой имеет вид Ax+By+C = 0, второй прямой - Dx+Ey+F = 0. Все коэффициенты (A, B, C, D, E, F) должны быть заданы.
Чтобы найти точку пересечения этих прямых нужно решить систему этих двух линейных уравнений.
Чтобы найти точку пересечения этих прямых нужно решить систему этих двух линейных уравнений.
2
Для решения первое уравнение удобно умножить на E, а второе - на B. В результате уравнения будут иметь вид: AEx+BEy+CE = 0, DBx+EBy+FB = 0. После вычитания второго уравнения из первого, получится: (AE-DB)x = FB-CE. Отсюда, x = (FB-CE)/(AE-DB).
По аналогии первое уравнение исходной системы можно умножить на D, второе - на A, затем опять из первого вычесть второго. В результате, y = (CD-FA)/(AE-DB).
Полученные значения x и y и будут координатами точки пересечения прямых.
По аналогии первое уравнение исходной системы можно умножить на D, второе - на A, затем опять из первого вычесть второго. В результате, y = (CD-FA)/(AE-DB).
Полученные значения x и y и будут координатами точки пересечения прямых.
3
Уравнения прямых также могут записываться через угловой коэффициент k, равный тангенсу угла наклона прямой. В этом случае уравнение прямой имеет вид y = kx+b. Пусть теперь уравнение первой прямой - y = k1*x+b1, а второй прямой - y = k2*x+b2.
4
Если приравнять правые части этих двух уравнений, то получится: k1*x+b1 = k2*x+b2. Отсюда легко получить, что x = (b1-b2)/(k2-k1). После подстановки этого значения x в любое из уравнений, получится: y = (k2*b1-k1*b2)/(k2-k1). Значения x и y будут задавать координаты точки пересечения прямых.
В случае, если две прямые параллельны или сопадают, то они не имеют общих точек или имеют бесконечно много общих точек соответственно. В этих случаях k1 = k2, знаменатели для координат точек пересечения будут обращаться в нуль, следовательно, система не будет иметь классического решения.
Система может иметь только одно классическое решение, что естественно, так как две несовпадающие и не параллельные друг другу прямые могут иметь только одну точку пересечения.
В случае, если две прямые параллельны или сопадают, то они не имеют общих точек или имеют бесконечно много общих точек соответственно. В этих случаях k1 = k2, знаменатели для координат точек пересечения будут обращаться в нуль, следовательно, система не будет иметь классического решения.
Система может иметь только одно классическое решение, что естественно, так как две несовпадающие и не параллельные друг другу прямые могут иметь только одну точку пересечения.