Инструкция
1
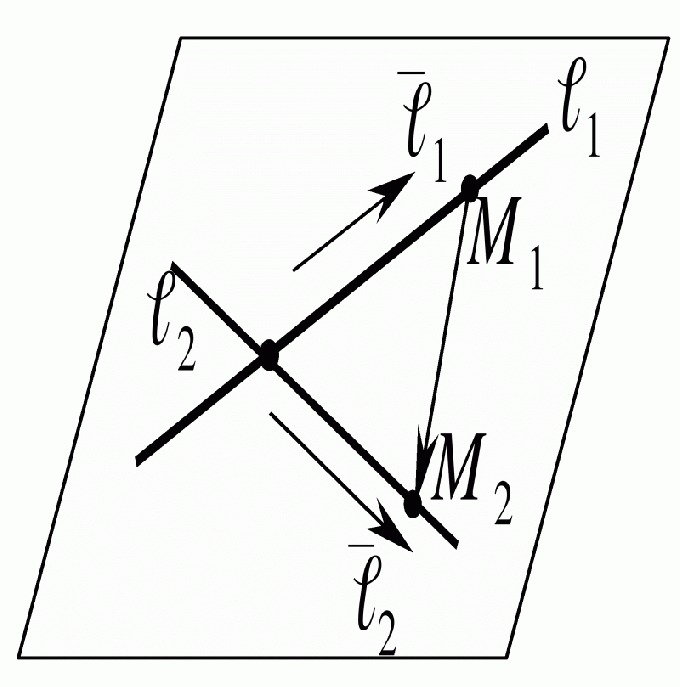
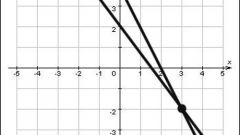
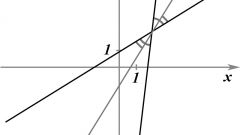
Запомните, что общее уравнение прямой в декартовых координатах имеет вид Ax+By+C = 0. Если прямые пересекаются, то уравнение первой из них можно записать соответственно как Ax+By+C = 0, а второй – в виде Dx+Ey+F = 0. Задайте все имеющиеся коэффициенты: A, B, C, D, E, F. Для нахождения точки пересечения прямых необходимо решить систему данных линейных уравнений. Сделать это можно несколькими способами.
2
Умножьте первое уравнение на E, а второе - на B. После этого уравнения должны выглядеть как: DBx+EBy+FB = 0, AEx+BEy+CE = 0. Далее вычтите второе уравнение из первого, чтобы получилось: (AE-DB)x = FB-CE. Вынесите коэффициент: x = (FB-CE)/(AE-DB).
3
Умножьте на D первое уравнение данной системы, а второе - на A, после чего нужно вновь вычесть второе из первого. В результате должно получиться уравнение: y = (CD-FA)/(AE-DB). Найдите x и y, и вы получите искомые координаты точки пересечения прямых.
4
Попробуйте записать уравнения прямых через угловой коэффициент k, который равен тангенсу угла пересечения прямых. При этом у вас получится уравнение: y = kx+b. Задайте для первой прямой равенство y = k1*x+b1, а для второй - y = k2*x+b2.
5
Приравняйте правые части двух уравнений, чтобы получилось: k1*x+b1 = k2*x+b2. Далее вынесите переменную: x = (b1-b2)/(k2-k1). Подставьте значение x в оба уравнения и получите: y = (k2*b1-k1*b2)/(k2-k1). Координаты точки пересечения будут задавать значения x и y.
Обратите внимание
Система обладает только одним классическим решением, поскольку две не параллельные и несовпадающие прямые имеют лишь одну точку пересечения. Если две прямые совпадают или параллельны, то у них нет общих точек или же их бесконечно много. В таких случаях k1 = k2, и знаменатели у координат точек пересечения всегда обращаются в нуль, поэтому классического решения данной системы не существует.