Инструкция
1
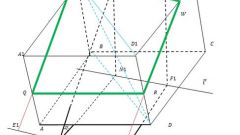
Прежде чем приступать к решению задачи, задайте исходные условия. В качестве объекта задачи используйте треугольную правильную призму ABC A1B1C1, в которой сторона AB=AA1 и равняется в свою очередь значению «b». Точка P является серединой стороны AA1, точка Q – серединой стороны основания BC.
2
Чтобы определить линию пересечения плоскости сечения с поверхностью призмы, примите допущение, что плоскость сечения проходит сквозь точки P и Q, а также, что она параллельна стороне призмы AC.
3
Учитывая данное допущение, постройте сечение секущей плоскости. Для чего проведите через точки P и Q прямые, которые будут параллельны стороне AC. В результате построения вы получите фигуру PNQM, которая и является сечением секущей плоскости.
4
Чтобы определить длину линии пересечения плоскости сечения с правильной треугольной призмой, необходимо определить периметр сечения PNQM. Для этого примите допущение, что PNQM представляет собой равнобокую трапецию. Сторона PN в равнобокой трапеции равняется стороне основания призмы AC и равняется условному значению «b». То есть PN = AC = b. Поскольку линия MQ является средней линией для треугольника ABC, следовательно, она равняется половине стороны AC. То есть MQ = 1/2AC = 1/2b.
5
Найдите значение другой стороны трапеции, используя теорему Пифагора. В данном случае сторона секущей плоскости PM является одновременной гипотенузой для прямоугольного треугольника PAM. Согласно теореме Пифагора PM = √(AP2+AM2) = (√2b)/2
6
Поскольку в равнобокой трапеции PNQM сторона PN = AC = b, сторона PM = NQ = (√2b)/2, а сторона MQ = 1/2b, то периметр секущей площади определяется сложением длин ее сторон. Получается следующая формула P=b+2*(√2b)/2+1/2b=1,5b+√2b. Значение периметра и будет искомой длиной линии пересечения плоскости сечения с поверхностью призмы.
Источники:
- как не пересекая линии