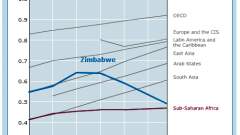
Инструкция
1
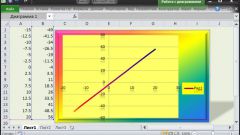
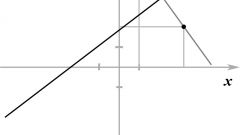
Чаще требуется строить прямую линию в плоскости. У каждой точки будет две координаты: х, y. Обратите внимание на уравнение прямой, оно подчиняется общему виду: y=k*x ±b, где k, b - свободные числа, а y, х – те самые координаты всех точек прямой.Из уравнения общего вида понятно, что для нахождения координаты y надо знать координату х. Самое интересное, что значение координаты х можно выбрать любое: из всей бесконечности известных чисел. Далее подставьте х в уравнение и, решив его, найдите у. Пример. Пусть дано уравнение: у=4х-3. Придумайте два любых значения для координат двух точек. К примеру, х1 = 1, х2 = 5.Подставьте эти значения в уравнения для нахождения координат у. у1 = 4*1 – 3 = 1. у2 = 4*5 – 3 = 17. Получились две точки А и В, с координатами А (1; 1) и В (5; 17).
2
Следует построить найденные точки в координатной оси, соединить их и увидеть ту самую прямую, которая была описана уравнением. Для построения прямой необходимо работать в декартовой системе координат. Начертите оси Х и У. В точке пересечения поставьте значение «ноль». Нанесите числа на оси.
3
В построенной системе отметьте две найденные в 1-м шаге точки. Принцип выставления указанных точек: точка А имеет координаты х1 = 1, у1 = 1; на оси Х выберите число 1, на оси У – число 1. В этой точке и находится точка А.Точка В задана значениями х2 = 5, у2 = 17. По аналогии найдите точку В на графике. Соедините А и В, чтобы получилась прямая.
Видео по теме