Инструкция
1
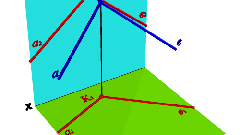
Если вам необходимо составить каноническое уравнение прямой, проходящей через некоторую точку M с координатами (Xm, Ym, Zm) и направляющим вектором a с координатами (r, s, t), то вам необходимо выполнить следующие действия.
2
Составьте систему параметрических уравнений прямой:X = Xm + r * pY = Ym + s * pZ = Zm + t * p,где p – некоторый произвольный параметр.Из этой системы выразите параметр p и получите требуемое каноническое уравнение прямой:p = (X - Xm)/r = (Y-Ym)/s = (Z - Zm)/t.
3
Пример. Пусть дана прямая, проходящая через точку M (2, 5, 0) и заданная направляющим вектором a = (4, 4, 1). Параметрическое уравнение для данной прямой будет следующим:(X – 2)/4 = (Y - 5)/4 = Z/1.
4
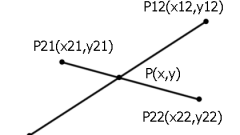
Если вам необходимо найти каноническое уравнение прямой, проходящей через две точки A (Ax, Ay, Az) и B (Bx, By, Bz), то запишите ту же систему параметрических уравнений, только для обеих точек A и B. X = Ax + r * p , Y = Ay + s * p, Z = Az + t * p X = Bx + r * p , Y = By + s * p, Z = Bz + t * p Выразите из первого уравнения первой системы параметр p: p = (X – Ax)/r. Из первого уравнения второй системы выразите коэффициент r: r = (X - Bx)/p. Далее подставьте значение для r в выражение для p: p = (X – Ax) * p/(X - Bx). Проделайте подобную операцию для всех уравнений системы. Сократив параметр p в числителе всех дробей, вы получите каноническое уравнение прямой, проходящей через две точки:(X – Ax) /(X - Bx) = (Y – Ay) /(Y - By) = (Z – Az) /(Z - Bz).
5
Пусть прямая проходит через точки A(1, 2, 3) и B(4, 5, 6). Тогда параметрическое уравнение будет иметь следующий вид:(X – 1) /(X – 4) = (Y – 2) /(Y - 5) = (Z – 3) /(Z - 6).