Вам понадобится
  • - карандаш;
  • - линейка;
  • - ручка;
  • - тетрадь;
  • - калькулятор.
Инструкция
1
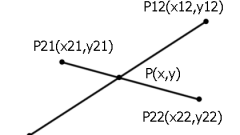
Проверить принадлежность точки той либо иной прямой довольно просто. Используйте для этого уравнение прямой. Итак, предположим, что прямая проходит через точки А(x1,y1) и В(x2,y2). Дана точка К(x,y): нужно проверить ее принадлежность прямой. Уравнение линии по двум точкам имеет следующий вид: (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) = 0.
2
Подставьте значение координат точки К в уравнение. Если (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) окажется больше нуля, то точка К расположена правее или ниже прямой, проведенной по точкам А и В.
3
В том случае, если (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) будет меньше нуля, точка К располагается выше или левее линии. Другими словами, только в том случае, если уравнение вида (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) = 0 справедливо, точки А, В и К будут расположены на одной прямой.
4
В остальных случаях лишь две точки (А и В), которые, по условию задания, лежат на прямой, будут ей принадлежать: через третью точку (точку К) прямая проходить не будет.
5
Рассмотрите второй вариант определения принадлежности точки примой: на этот раз нужно проверить принадлежит ли точка С(x,y) отрезку с концевыми точками В(x1,y1) и А(x2,y2), который является частью прямой z.
6
Точки рассматриваемого отрезка опишите уравнением pOB+(1-p)OА=z, при условии, что 0≤p≤1. ОВ и ОА являются векторами. Если есть такое число p, которое больше или равно 0, но меньше или равно 1, то pOB+(1-p)OА=С, а значит, точка С будет лежать на отрезке АВ. В противном случае, данная точка не будет принадлежать этому отрезку.
7
Распишите равенство pOB+(1-p)OА=С покоординатно: px1+(1-p)x2=x и py1+(1-p)y2=y.
8
Найдите из первого уравнения число р и подставьте его значение во второе равенство. Если равенство будет соответствовать условиям 0≤p≤1, то точка С принадлежит отрезку АВ.
9
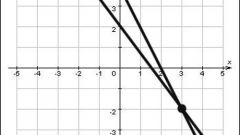
Постройте точки по заданным координатам и проведите через них прямую. Это позволит увидеть точки, лежащие на одной прямой, и те точки, что не принадлежат ей.