Вам понадобится
- учебник по геометрии, лист бумаги, карандаш
Инструкция
1
Откройте учебник по геометрии на главе «Векторы» и повторите основные принципы векторной алгебры. Для построения плоскости по трем точкам потребуется знание таких тем, как линейное пространство, ортонормированный базис, коллинеарность векторов, а также понимание принципов линейной алгебры.
2
Вспомните, что через три заданные точки, если они не лежат на одной прямой, можно провести только одну плоскость. Это означает, что наличие трех конкретных точек в линейном пространстве уже однозначно определяет единственную плоскость.
3
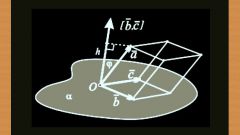
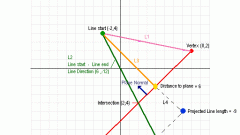
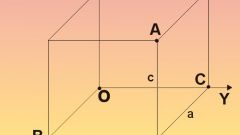
Задайте в трехмерном пространстве три точки, имеющие различные координаты: x1, y1, z1, x2, y2, z2, x3, y3, z3. Будет использоваться общее уравнение плоскости, подразумевающее известность какой-либо одной точки, например, точки с координатами x1,y1,z1, а также знание координат нормального к данной плоскости вектора. Таким образом, общий принцип построения плоскости будет заключаться в том, что скалярное произведение любого вектора, лежащего в плоскости, и нормального вектора должно быть равно нулю. Отсюда и получается общее уравнение плоскости a(x-x1)+b(y-y1)+c(z-z1)=0, где коэффициенты a, b и c – это компоненты вектора, перпендикулярного плоскости.
4
В качестве вектора, лежащего в самой плоскости, можете взять любой вектор, построенный на любых двух точках из тех трех, что известны изначально. Координаты данного вектора будут иметь вид (x2-x1), (y2-y1), (z2-z1). Соответствующий вектор можно назвать m2m1.
5
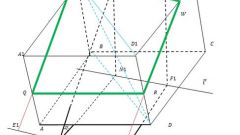
Определите нормальный вектор n посредством векторного произведения двух векторов, лежащих в данной плоскости. Как известно, векторное произведение двух векторов – это всегда вектор, перпендикулярный обоим векторам, по которым он строится. Таким образом, можно получить новый вектор, перпендикулярный всей плоскости. В качестве двух векторов, лежащих в плоскости, можно взять любой из векторов m3m1, m2m1, m3m2, построенных по тому же принципу, что и вектор m2m1.
6
Найдите векторное произведение векторов, лежащих в одной плоскости, определив таким образом нормальный вектор n. Помните, что векторное произведение – это, фактически, определитель второго порядка, первая строка которого содержит орты i, j, k, вторая строка – компоненты первого вектора векторного произведения, а третья – компоненты второго вектора. Раскрыв определитель, вы получите компоненты вектора n, то есть a, b и с, которые и задают плоскость.