Вам понадобится
  • Точки, заданные координатами.
Инструкция
1
Если вам даны точки с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), найдите уравнение прямой, используя координаты любых двух точек, например, первой и второй. Для этого подставьте соответствующие значения в уравнение прямой: (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, просто приравняйте к нулю числитель.
2
Найти уравнение прямой, зная две точки с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).
3
Получив уравнение прямой, проходящей через две точки, подставьте значения координат третьей точки в него вместо переменных х и у. Если равенство получилось верное, значит все три точки лежат на одной прямой. Точно так же можете проверять принадлежность этой прямой других точек.
4
Проверьте принадлежность всех точек прямой, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.
5
Еще один способ проверить принадлежность трех точек прямой – посчитайте площадь треугольника, который они образуют. Если все точки лежат на прямой, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если после всех вычислений вы получили ноль - значит, три точки лежат на одной прямой.
6
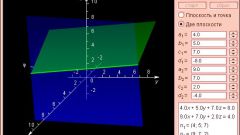
Чтобы найти решение задачи графическим способом, постройте координатные плоскости и найдите точки по указанным координатам. Затем проведите прямую через две из них и продолжите до третьей точки, посмотрите, пройдет ли она через нее. Учтите, этот способ подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой способ неприменим.