Как найти нормаль

Под математическим термином нормаль прячется более привычное на слух понятие перпендикуляра. То есть задача нахождения нормали подразумевает поиск уравнения прямой, перпендикулярной к заданной кривой или поверхности, проходящей через определенную точку. В зависимости от того, на плоскости или в пространстве требуется найти нормаль, данная задача решается по-разному. Рассмотрим оба варианта задачи.

Вам понадобится

• умение находить производные функции, умение находить частные производные функции нескольких переменных

Инструкция

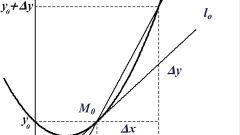
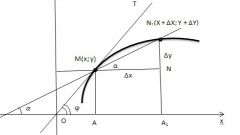
1. Нормаль к кривой, заданной на плоскости в виде уравнения у = f(x).Находим значение функции, которая определяет уравнение данной кривой в точке, в которой ищется уравнение нормали: а = f(x0). Находим производную к данной функции: f'(x). Ищем значение производной в этой же точке: B = f'(x0). Вычисляем значение следующего выражения: C = a – B*x0. Составляем уравнение нормали, которое будет иметь вид: у = B*x + C.
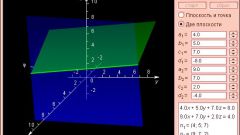
2. Нормаль к поверхности или кривой, заданной в пространстве в виде уравнения f = f(x,y,z).Находим частные производные к данной нам функции: f'x(x,y,z), f’y(x,y,z), f’z(x,y,z). Ищем значение этих производных в точке М(x0,y0,z0) – точка, в которой надо найти уравнение нормали к поверхности или пространственной кривой: A = f'x(x0,y0,z0), B = f’y(x0,y0,z0), C = f’z(x0,y0,z0). Составляем уравнение нормали, которое будет иметь вид: (x – x0)/A = (y – y0)/B = (z – z0)/C
3. Пример:
   Найдем уравнение нормали к функции у = х – х^2 в точке х = 1.
   Значение функции в данной точке а = 1 – 1 = 0.
   Производная к функции у' = 1 – 2х, в данной точке В = у'(1) = -1.
   Вычисляем С = 0 – (-1)*1 = 1.
   Искомое уравнение нормали имеет вид: у = -х + 1