Инструкция
1
Справочный материал.
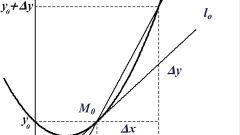
Для начала дадим определение касательной. Касательной к кривой в данной точке М называется предельное положение секущей NM, когда точка N приближается вдоль кривой к точке М.
Найдем уравнение касательной к графику функции y = f(x).
Для начала дадим определение касательной. Касательной к кривой в данной точке М называется предельное положение секущей NM, когда точка N приближается вдоль кривой к точке М.
Найдем уравнение касательной к графику функции y = f(x).
2
Определяем угловой коэффициент касательной к кривой в точке М.
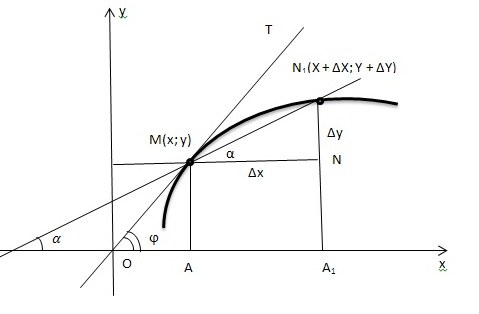
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).
Проведем секущую MN1, образующую с положительным направлением оси Ox угол α.
Координаты точки М (x; y), координаты точки N1(x+∆x; y+∆y).
Из полученного треугольника MN1N можно найти угловой коэффициент этой секущей:
tg α = Δy/Δx
MN = ∆x
NN1 = ∆y
При стремлении точки N1 по кривой к точке M секущая MN1 поворачивается вокруг точки M, причем угол α стремится к углу ϕ между касательной MT и положительным направлением оси Ox.
k = tg ϕ =〖 lim〗┬(∆x→0)〖 〗 Δy/Δx = f`(x)
Таким образом, угловой коэффициент касательной к графику функции равен значению производной этой функции в точке касания. В этом заключается геометрический смысл производной.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).
Проведем секущую MN1, образующую с положительным направлением оси Ox угол α.
Координаты точки М (x; y), координаты точки N1(x+∆x; y+∆y).
Из полученного треугольника MN1N можно найти угловой коэффициент этой секущей:
tg α = Δy/Δx
MN = ∆x
NN1 = ∆y
При стремлении точки N1 по кривой к точке M секущая MN1 поворачивается вокруг точки M, причем угол α стремится к углу ϕ между касательной MT и положительным направлением оси Ox.
k = tg ϕ =〖 lim〗┬(∆x→0)〖 〗 Δy/Δx = f`(x)
Таким образом, угловой коэффициент касательной к графику функции равен значению производной этой функции в точке касания. В этом заключается геометрический смысл производной.
3
Уравнение касательной к заданной кривой в заданной точке М имеет вид:
y - y0 = f`(x0) (x - x0),
где (x0; y0) – координаты точки касания,
(x; y) – текущие координаты, т.е. координаты любой точки, принадлежащей касательной,
f`(x0) = k = tg α – угловой коэффициент касательной.
y - y0 = f`(x0) (x - x0),
где (x0; y0) – координаты точки касания,
(x; y) – текущие координаты, т.е. координаты любой точки, принадлежащей касательной,
f`(x0) = k = tg α – угловой коэффициент касательной.
4
Найдем уравнение касательной на примере.
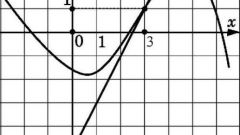
Дан график функции y=x2 – 2x. Нужно найти уравнение касательной в точке с абсциссой x0 = 3.
Из уравнения данной кривой находим ординату точки касания y0 = 32 - 2∙3 = 3.
Находим производную, а затем вычисляем ее значение в точке x0 = 3.
Имеем:
y`=2x – 2
f`(3) = 2∙3 – 2 = 4.
Теперь, зная точку (3; 3) на кривой и угловой коэффициент f`(3) = 4 касательной в этой точке, получаем искомое уравнение:
y – 3 = 4 (x – 3)
или
y – 4x + 9 = 0
Дан график функции y=x2 – 2x. Нужно найти уравнение касательной в точке с абсциссой x0 = 3.
Из уравнения данной кривой находим ординату точки касания y0 = 32 - 2∙3 = 3.
Находим производную, а затем вычисляем ее значение в точке x0 = 3.
Имеем:
y`=2x – 2
f`(3) = 2∙3 – 2 = 4.
Теперь, зная точку (3; 3) на кривой и угловой коэффициент f`(3) = 4 касательной в этой точке, получаем искомое уравнение:
y – 3 = 4 (x – 3)
или
y – 4x + 9 = 0
Видео по теме