Касательная к окружности в двумерном пространстве - прямая, имеющая с окружностью только одну общую точку. В общем случае касательная - прямая, с которой стремится совпасть секущая, проведенная через две точки на произвольной кривой по мере сближения этих точек.
Первым свойством касательной к окружности является ее перпендикулярность радиусу этой окружности. Поэтому для начала нужно построить радиус окружности, который соединит центр окружности и точку на окружности, через которую нужно провести касательную.
2
Далее необходимо построить прямую, проходящую через эту точку на окружности и перпендикулярную радиусу. Это можно сделать несколькими способами. Легче всего построить перпендикулярную прямую с помощью транспортира, отложив прямую под углом 90 градусов к радиусу.
3
Можно воспользоваться и угольником. Для этого нужно совместить радиус с одной из сторон угольника так, чтобы точка на окружности совпала с точкой пересечения двух сторон угольника. Тогда другая сторона угольника совпадет с касательной.
4
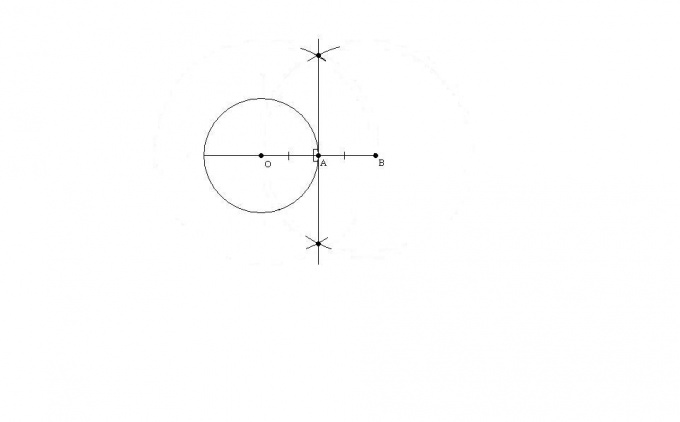
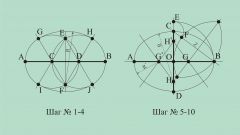
Если нет ни угольника, ни транспортира, то можно использовать циркуль. Для этого радиус окружности нужно продлить на длину, равную радиусу, наружу. Получится отрезок, равный по длине двум радиусам окружности с концами в центре окружности O и с точкой B вне окружности. Точка A на окружности окажется центром этой окружности.
5
Для построения касательной (перпендикулярной прямой) нужно построить две окружности - с центром в точке O и радиусом OB и с центром в точке B и радиусом OB. Две полученные окружности пересекутся дважды. Соединив точку A с любой из двух точек пересечения получившихся окружностей, вы получите касательную.
Видео по теме
Источники:
Точка касания лежит на перпендикуляре, проведенном из центра
