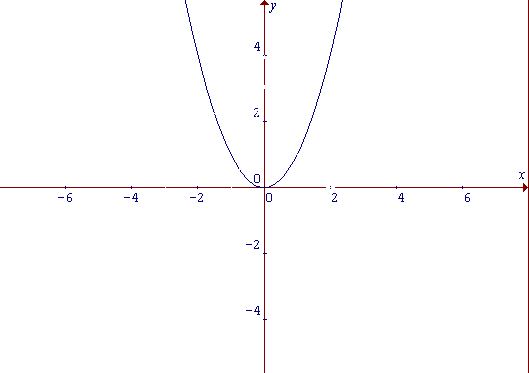Инструкция
1
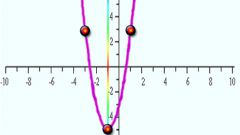
Парабола представляет собой кривую, которая по своей форме напоминает дугу и является графиком степенной функции. Независимо от того, какие характеристики имеет парабола, эта функция является четной. Четной называется такая функция, у которой при всех значениях аргумента из области определения при изменении знака аргумента значение не изменяется:f(-x)=f(x)Начните с самой простую функции: y=x^2. Из ее вида можно сделать вывод, что она возрастает как при положительных, так и при отрицательных значениях аргумента x. Точка, в которой x=0, и при этом, y =0 считается точкой минимума функции.
2
Ниже приведены все основные варианты построения этой функции и ее уравнение. В качестве первого примера ниже рассмотрена функция вида:f(x)=x^2+a, где a - целое числоДля того, чтобы построить график данной функции, необходимо сдвинуть график функции f(x) на a единиц. Примером может служить функция y=x^2+3, где вдоль оси y сдвигают функцию вверх на две единицы. Если дана функция с противоположным знаком, например y=x^2-3, то ее график сдвигают вниз по оси y.
3
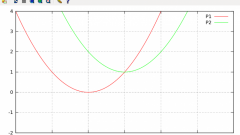
Еще один вид функции, которой может быть задана парабола - f(x)=(x +a)^2. В таких случаях график, наоборот, сдвигается вдоль оси абсцисс (оси x) на a единиц. Для примера можно рассмотреть функции: y=(x +4)^2 и y=(x-4)^2. В первом случае, где имеется функция со знаком плюс, график сдвигают по оси x влево, а во втором случае - вправо. Все эти случаи показаны на рисунке.
4
Существуют также параболические зависимости вида y=x^4. При таких случаях x=const, а y резко возрастает. Однако, это касается только четных функций.Графики параболы часто присутствуют и в физических задачах, например, полет тела описывает линию, похожую именно на параболу. Также вид параболы имеет продольное сечение рефлектора фары, фонаря. В отличие от синусоиды, этот график является непериодическим и возрастающим.