Инструкция
1
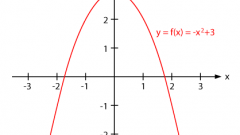
Первым пунктом запишите область определения функции D(y). Парабола определена на всей числовой прямой, если не задано никаких дополнительных условий. Обычно это указывается записью D(y)=R, где R – множество всех действительных чисел.
2
Найдите вершину параболы. Координата по оси абсцисс x0=-B/2A. Подставьте x0 в уравнение параболы и сосчитайте координату вершины по оси ординат Oy. Итак, вторым пунктом должна появится запись: (x0;y0) – координаты вершины параболы. Естественно, вместо x0 и y0 у вас должны быть конкретные числа. Отметьте эту точку на чертеже.
3
Сравнивая старший коэффициент A при x² с нулем, сделайте вывод о направлении ветвей параболы. Если A>0, то ветви параболы направлены вверх. При отрицательном значении числа A ветви параболы направлены вниз.
4
Теперь вы можете найти множество значений функции E(y). Если ветви направлены вверх, функция y принимает все значения выше y0. При направлении ветвей вниз функция принимает значения ниже y0. Для первого случая запишите: E(y)=[y0,+∞), для второго – E(y)=(-∞;y0]. Квадратная скобка говорит о том, что крайнее число включается в промежуток.
5
Напишите уравнение для оси симметрии параболы. Оно будет иметь вид: x=x0 и проходить через вершину. Начертите эту ось строго перпендикулярно оси Ox.
6
Найдите «нули» функции. Эти точки будут пересекать координатные оси. Приравняйте x нулю и посчитайте y для этого случая. Затем найдите, при каких значениях аргумента функция y обратится в нуль. Для этого решите квадратное уравнение A·x²+B·x+C=0. Отметьте точки на графике.
7
Найдите дополнительные точки для построения параболы. Оформите в виде таблицы. Первой строкой записывайте аргумент x, второй – функцию y. Лучше подбирать такие числа, для которых x и y будут целыми, т.к. дробные числа изображать неудобно. Полученные точки отметьте на графике.