Инструкция
1
Для того чтобы вычислить функцию и построить график, нужно выполнить следующие действия: найти область определения, проанализировать поведение функции на границах этой области (вертикальные асимптоты), исследовать на четность, определить промежутки выпуклости и вогнутости, выявить наклонные асимптоты и рассчитать промежуточные значения.
2
Область определения
Первоначально предполагается, что ею является бесконечный интервал, затем на него накладываются ограничения. Если в выражении функции встречаются следующие подфункции, решите соответствующие неравенства. Их совокупный результат и будет областью определения:
• Корень четной степени от Φ с показателем в виде дроби с четным знаменателем. Выражение, стоящее под его знаком, может быть только положительным или нулем: Φ ≥ 0;
• Логарифмическое выражение вида log_b Φ → Φ> 0;
• Две тригонометрические функции тангенс и котангенс. Их аргумент – мера угла, которая не может быть равной π•k + π/2, иначе функция не имеет смысла. Итак, Φ ≠ π•k + π/2;
• Арксинус и арккосинус, которые имеют строгую область определения -1 ≤ Φ ≤ 1;
• Степенная функция, показатель которой – другая функция: Φ^f → Φ > 0;
• Дробь, образованная отношением двух функций Φ1/Φ2. Очевидно, что Φ2 ≠ 0.
Первоначально предполагается, что ею является бесконечный интервал, затем на него накладываются ограничения. Если в выражении функции встречаются следующие подфункции, решите соответствующие неравенства. Их совокупный результат и будет областью определения:
• Корень четной степени от Φ с показателем в виде дроби с четным знаменателем. Выражение, стоящее под его знаком, может быть только положительным или нулем: Φ ≥ 0;
• Логарифмическое выражение вида log_b Φ → Φ> 0;
• Две тригонометрические функции тангенс и котангенс. Их аргумент – мера угла, которая не может быть равной π•k + π/2, иначе функция не имеет смысла. Итак, Φ ≠ π•k + π/2;
• Арксинус и арккосинус, которые имеют строгую область определения -1 ≤ Φ ≤ 1;
• Степенная функция, показатель которой – другая функция: Φ^f → Φ > 0;
• Дробь, образованная отношением двух функций Φ1/Φ2. Очевидно, что Φ2 ≠ 0.
3
Вертикальные асимптоты
Если они есть, то располагаются на границах области определения. Чтобы это выяснить, решите односторонние пределы при х → A-0 и х → В+0, где х – аргумент функции (абсцисса графика), А и В – начало и конец интервала области определения. Если таких интервалов несколько, исследуйте все их граничные значения.
Если они есть, то располагаются на границах области определения. Чтобы это выяснить, решите односторонние пределы при х → A-0 и х → В+0, где х – аргумент функции (абсцисса графика), А и В – начало и конец интервала области определения. Если таких интервалов несколько, исследуйте все их граничные значения.
4
Четность/нечетность
Подставьте в выражение функции аргумент (-х) вместо х. Если результат не изменится, т.е. Φ(-х) = Φ(х), то она четная, если же Φ(-х) = -Φ(х), – нечетная. Это необходимо для того, чтобы выявить наличие симметрии графика относительно оси ординат (четность) или начала координат (нечетность).
Подставьте в выражение функции аргумент (-х) вместо х. Если результат не изменится, т.е. Φ(-х) = Φ(х), то она четная, если же Φ(-х) = -Φ(х), – нечетная. Это необходимо для того, чтобы выявить наличие симметрии графика относительно оси ординат (четность) или начала координат (нечетность).
5
Возрастание/убывание, точки экстремума
Вычислите производную функции и решите два неравенства Φ’(х) ≥ 0 и Φ’(х) ≤ 0. В результате вы получите промежутки возрастания/убывания функции. Если в какой-то точке производная обращается в ноль, то она называется критической. Возможно, она также является точкой перегиба, выясните это в следующем действии.
Вычислите производную функции и решите два неравенства Φ’(х) ≥ 0 и Φ’(х) ≤ 0. В результате вы получите промежутки возрастания/убывания функции. Если в какой-то точке производная обращается в ноль, то она называется критической. Возможно, она также является точкой перегиба, выясните это в следующем действии.
6
В любом случае это точка экстремума, в которой происходит перелом, смена одного состояния на другое. Например, если убывающая функция становится возрастающей, то это точка минимума, если наоборот – максимума. Обратите внимание, что производная может иметь свою область определения, более строгую.
7
Выпуклость/вогнутость, точки перегиба
Найдите вторую производную и решите аналогичные неравенства Φ’’(х) ≥ 0 и Φ’’(х) ≤ 0. На этот раз результатами будут интервалы выпуклости и вогнутости графика. Точки, в которых вторая производная равна нулю, являются стационарными и могут быть точками перегиба. Проверьте, как ведет себя функция Φ’’ до и после них. Если меняет знак, значит, это точка перегиба. Кроме того, проверьте на это свойство критические точки, определенные в предыдущем действии.
Найдите вторую производную и решите аналогичные неравенства Φ’’(х) ≥ 0 и Φ’’(х) ≤ 0. На этот раз результатами будут интервалы выпуклости и вогнутости графика. Точки, в которых вторая производная равна нулю, являются стационарными и могут быть точками перегиба. Проверьте, как ведет себя функция Φ’’ до и после них. Если меняет знак, значит, это точка перегиба. Кроме того, проверьте на это свойство критические точки, определенные в предыдущем действии.
8
Наклонные асимптоты
Асимптоты – большие помощники при построении графика. Это прямые линии, к которым приближается бесконечная ветвь кривой функции. Они задаются уравнением у = k•х + b, где коэффициент k равен пределу lim Φ/х при х→ ∞, а слагаемое b – такому же пределу выражения (Φ – k•х). При k=0 асимптота проходит горизонтально.
Асимптоты – большие помощники при построении графика. Это прямые линии, к которым приближается бесконечная ветвь кривой функции. Они задаются уравнением у = k•х + b, где коэффициент k равен пределу lim Φ/х при х→ ∞, а слагаемое b – такому же пределу выражения (Φ – k•х). При k=0 асимптота проходит горизонтально.
9
Вычисление в промежуточных точках
Это вспомогательное действие, чтобы добиться большей точности построения. Подставьте несколько любых значений из области определения в функцию.
Это вспомогательное действие, чтобы добиться большей точности построения. Подставьте несколько любых значений из области определения в функцию.
10
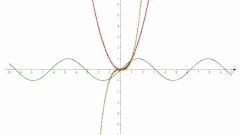
Построение графика
Начертите асимптоты, нанесите экстремумы, отметьте точки перегибов и промежуточные точки. Схематично покажите промежутки возрастания и убывания, выпуклости и вогнутости, например, знаками «+», «-» или стрелками. Проведите линии графика по всем точкам, приблизьте к асимптотам, изгибая в соответствии со стрелками или знаками. Проверьте симметрию, выявленную на третьем шаге.
Начертите асимптоты, нанесите экстремумы, отметьте точки перегибов и промежуточные точки. Схематично покажите промежутки возрастания и убывания, выпуклости и вогнутости, например, знаками «+», «-» или стрелками. Проведите линии графика по всем точкам, приблизьте к асимптотам, изгибая в соответствии со стрелками или знаками. Проверьте симметрию, выявленную на третьем шаге.