Инструкция
1
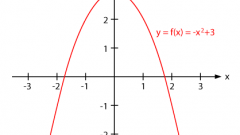
Поскольку любая функция – это линейная или нелинейная зависимость от аргумента, постарайтесь представить функцию в стандартном виде y=f(x), где f(x) – это функция, x – аргумент, а y – значение функции. Таким образом, каждому конкретному значению аргумента соответствует конкретное значение функции.
2
Найдите область определения функции, а также точки пересечения функции с осями абсцисс и ординат. Для этого вычислите значение функции при x=0, затем посчитайте, при каком значении аргумента значение функции будет равно нулю.
3
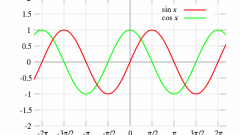
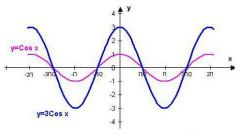
Исследуйте функцию на симметричность. Функция будет четной, если для каждого x из ее области определения выполняется равенство f(-x)=f(x), и нечетной, если выполняется неравенство f(-x)=-f(x). Следует также определить периодичность функции. Если для каждого x из области определения функции выполняется равенство f(T+x)=f(x), где T – период функции, то ее считают периодической. К таким функциям относятся функции f(x)=sin(x), f(x)=cos(x) и т.п.
4
Определите точки разрыва функции, если таковые имеются. Постройте вертикальные, горизонтальные и наклонные асимптоты.
5
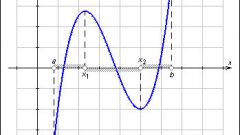
Найдите производную функции, а затем точки экстремума (максимума и минимума функции). Приравняйте производную к нулю и найдите абсциссу точки экстремума. Затем подставьте ее в уравнение функции и найдите ординату точки экстремума. Найдите интервалы, в которых функция монотонна (убывает или возрастает на всем интервале).
6
Исследуйте функцию по второй производной для того, чтобы определить точки перегиба функции. Для этого приравняйте вторую производную функции к нулю и найдите абсциссу точки перегиба функции. Ординату можно найти, подставив полученное значение в уравнение функции.
7
Начертите на бумаге в клетку или на миллиметровой бумаге взаимно перпендикулярные оси координат x и y, которые пересекаются в точке с координатами (0; 0). Отложите все найденные в процессе исследования функции точки в системе координат. Чтобы график функции был изображен точнее, вычислите значения функции, подставив еще несколько значений аргумента. Соедините полученные точки плавной линией (прямой или кривой). Для аккуратного построения графика пользуйтесь лекалами.