Как построить функцию

Функция – математическое выражение, в котором определяется зависимость одной переменной от другой или отражается связь между элементами разных множеств. В этом случае одному значению множества соответствует определенное значение другого. Обычно функция задается уравнением, решая которое, можно определить область ее значения - те значения переменной, при которой алгебраическое уравнение имеет смысл.

Инструкция

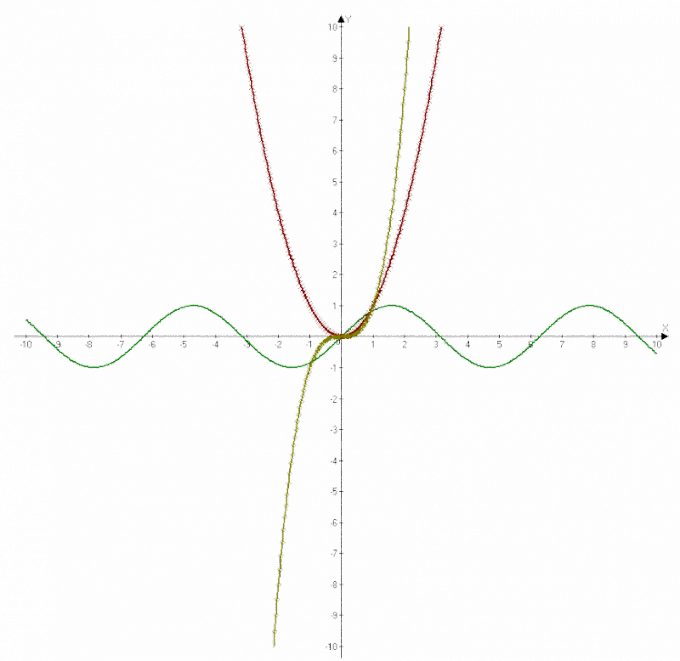
1. Уравнение записывают в виде формулы, в левой части которой находится искомая величина у, а в правой части - выражение, в котором необходимо найти значение переменной х. График функции обычно строится в прямоугольной системе координат. Уравнение определяет и название функции. Линейная функция, например, определяется уравнением простой зависимости у от х. График такой функции представляет собой прямую линию. Парабола является графическим решением квадратного уравнения. Тригонометрические функции в графическом изображении представляют собой рассчитанные кривые.
2. Чтобы построить график функции. Задайте числовые значения переменной х, получите значения искомого у, запишите результаты в таблицу, где каждому х будет соответствовать определенное у.
3. Постройте на листе миллиметровой бумаги или странице в клетку систему координат, которая образуется пересекающимися горизонтальной и вертикальной прямыми. Задайте абсциссу х (горизонтальная прямая) и ординату у (вертикальная прямая), обозначьте на их пересечении точку О – начало координат. Выберите на каждой оси положительное направление, укажите его стрелками (по абсциссе - вправо, по ординате – вверх), задайте единицы измерения, обозначив равные отрезки цифрами по порядку.
4. В соответствии с созданной таблицей найдите на координатной плоскости точки, координаты которых будут удовлетворять условиям уравнения. Обозначите точки буквами или цифрами.
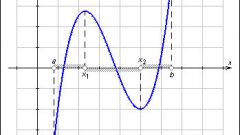
5. Соедините найденные точки непрерывной линией. Если значение переменной х или у будут равны 0, значит, график будет пересекать оси координат. При присутствии в уравнении постоянной величины n, график будет смещен на n единиц относительно осей координат.
6. Навыкам исследования функций и построению графиков сегодня обучают в 8 классе средней школы. Однако с усложнением функций, их решений, усложняется и построение графиков.
7. Существует множество компьютерных программ, позволяющих построить различные графики самых сложных функций. Но элементарные знания в решении функций и построении их графиков необходимы каждому учащемуся.