Инструкция
1
На единичной тригонометрической окружности синус угла определяется отношением ординаты “y” к радиусу R. Поскольку R=1, можно рассматривать просто ординату “y”. Она соответствует двум точкам на этой окружности.
2
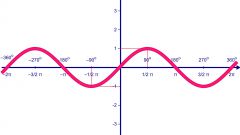
Для будущей синусоиды постройте координатные оси Ox и Oy. На оси ординат отметьте точки 1 и -1. Отрезок для единицы выберите большой, так как за его пределы функция синуса не зайдет. На оси абсцисс выберите масштаб, равный π/2. π/2 примерно равно 1,5, число π примерно равно трем.
3
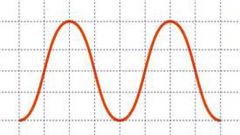
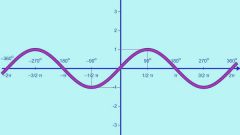
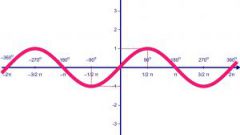
Найдите ключевые точки синусоиды. Посчитайте значение функции для аргумента, равного нулю, п/2, п, 3п/2. Так, sin0=0, sin(п/2)=1, sin(п)=0, sin(3п/2)=-1, sin(2п)=0. Легко видеть, что функция синуса имеет период, равный 2п. То есть через числовой промежуток в 2п значения функции повторяются. Поэтому для исследования свойств синуса достаточно построить график на одном из таких отрезков.
4
5
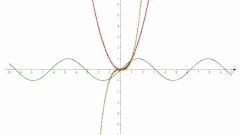
Осталось лишь плавно соединить полученные точки на графике. Выше оси Ox синусоида будет выпуклая, ниже – вогнутая. Точки, в которых синусоида пересекает ось абсцисс, являются точками перегиба функции. Вторая производная в этих точках равна нулю. Имейте в виду, что в концах отрезка синусоида не заканчивается, она бесконечна.
Полезный совет
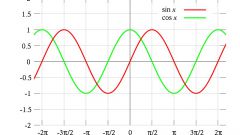
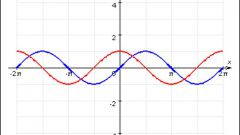
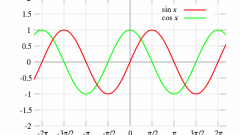
Из графика синуса легко можно получить график функции косинуса. Для этого сместите синусоиду на п/2 влево. Смещать можно не саму синусоиду, а координатные оси, только уже вправо.
Источники:
- sin 2п 3