Вам понадобится
- - карандаш или ручка;
- - лист бумаги;
- - линейка.
Инструкция
1
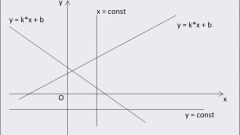
Для того чтобы начертить прямую, необходимы две точки. Именно с них начинается построение линии. У каждой точки на плоскости есть две координаты: х и у. Они будут являться параметрами уравнения прямой: у = k*х ±b, где k и b – это свободные числа, х и у – координаты точек прямой.
2
Для того чтобы найти координату у, вам необходимо задать некоторое значение для координаты х и подставить ее в уравнение. При этом значение координаты х может быть любым из всей бесконечности чисел, как положительным, так и отрицательным. Благодаря уравнению прямой, можно не только построить нужную вам прямую линию, но и узнать, под каким углом она расположена, в какой части координатной плоскости находится, является она убывающей или возрастающей.
3
Рассмотрите такой пример. Пусть дано уравнение: у = 3х-2. Возьмите два любых значения для координаты х, допустим х1 = 1, х2 = 3. Подставьте эти значения в уравнение прямой: у1 = 3*1-2 = 1, у2 = 3*3-2 = 7. В вас получатся две точки с различными координатами: А (1;1), В (3;7).
4
Затем отложите полученный точки на координатной оси, соедините их и вы увидите прямую, которую необходимо было построить по заданному уравнению. Предварительно вам следует начертить в декартовой системе координат оси Х (ось абсцисс), расположенную горизонтально, и У (ось ординат), расположенную вертикально. На пересечении осей отметьте «ноль». Затем отложите числа по горизонтали и вертикали.
5
После этого переходите к построению. Принцип построения довольно прост. Сначала отметьте первую точку А. Для этого отложите на оси Х число 1 и на оси У это же число, поскольку точка А имеет координаты (1;1). Аналогичным образом постройте точку В, отложив по оси Х три единицы, а по оси У – семь. Вам останется только в помощью линейки соединить полученные точки и получить требуемую прямую.