Как построить график линейной функции

Линейной функцией называется функция вида y = k * x + b. Графически она изображается прямой линией. Функции такого вида широко применяются в физике и технике для представления зависимостей между различными величинами.

Инструкция

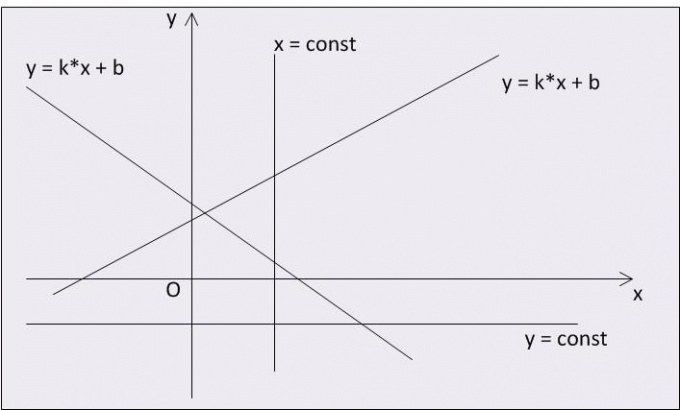
1. Пусть дана функция общего вида y = k * x + b, где k ≠ 0, b ≠ 0. Для построения графика линейной функции достаточно двух точек. Для наглядности и точности построения найдите пять точек заданной функции: x = -1; 0; 1; 3; 5. Подставьте эти значения в заданное выражение для функции и вычислите значения y: y = -k + b; b; k + b; 3 * k + b; 5 * k + b. Далее нарисуйте горизонтальную ось абсцисс (ось x) и вертикальную ось ординат (ось y). Отметьте на получившейся координатной плоскости найденные пары точек (-1, -k + b), (0, b), (1, k + b), (3, 3 * k + b), (5, 5 * k + b). Для этого сначала найдите требуемое значение на оси x, а затем отложите соответствующее значение на оси y. Потом проведите прямую линию, соединяющую все обозначенные точки.
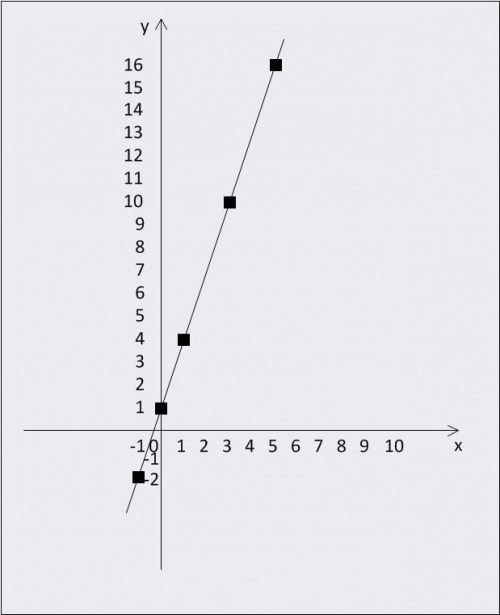
2. Постройте график следующей функции: y = 3 * x + 1. Вычислите значения координат y для следующих точек x = -1, 0, 1, 3, 5. Например, для точки с координатой x = -1: y = 3 * (-1) + 1 = -3 + 1 = -2. Получается точка (-1, -2). Аналогично для других точек: (0, 1), (1, 4), (3, 10), (5, 16). Теперь отметьте эти точки на координатной плоскости. Через получившиеся точки проведите прямую линию.
   
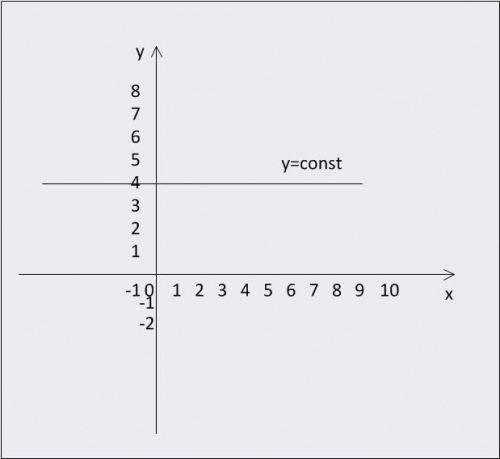
3. Для линейных функций возможны частные случаи. Обратите внимание на самые распространенные. Во-первых, y = const. В данном примере значение координаты y постоянно для любого значения координаты x. В традиционной системе координат (ось x – горизонтальная, ось y – вертикальная) график подобной функции выглядит как горизонтальная прямая линия.
   
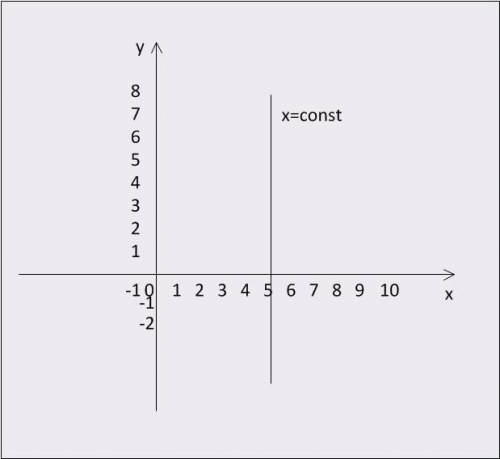
4. Во-вторых, x = const. Здесь для любого значения координаты y значение x всегда постоянное. Т.е. график выглядит как вертикальная прямая линия.