Инструкция
1
Можно рассмотреть примерную схему, по которой целесообразно исследовать поведение функции и строить ее график.
Найдите область определения функции. Определите, является ли функция четной и нечетной. В случае нахождения нужного ответа, продолжите исследование только на требуемой полуоси. Определите, является ли функция периодической. В случае положительного ответа продолжите исследование только на одном периоде. Найдите точки разрыва функции и определите ее поведение в окрестности этих точек.
Найдите область определения функции. Определите, является ли функция четной и нечетной. В случае нахождения нужного ответа, продолжите исследование только на требуемой полуоси. Определите, является ли функция периодической. В случае положительного ответа продолжите исследование только на одном периоде. Найдите точки разрыва функции и определите ее поведение в окрестности этих точек.
2
Найдите точки пересечения графика функции с осями координат. Найдите асимптоты, если они есть. Исследуйте с помощью первой производной функцию на экстремумы и интервалы монотонности. Также проведите исследование с помощью второй производной на выпуклость, вогнутость и точки перегиба. Выберите точки для уточнения поведения функции и вычислите в них значения функции. Постройте график функции, учитывая полученные результаты по всем проведенным исследованиям.
3
На оси 0Х следует выделить характерные точки: точки разрыва, х=0 , нули функции, точки экстремума, точки перегиба. В этих асимптот, и даст эскиз графика функции.
4
Так, на конкретном примере функции y=((x^2)+1)/(x-1) проведите исследование с помощью первой производной. Перепишите функцию в виде y=x+1+2/(x-1). Первая производная будет равна y’=1-2/((x-1)^2).
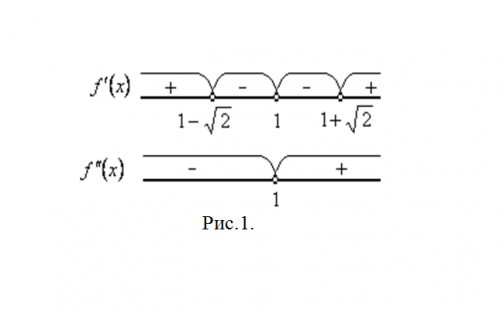
Найдите критические точки первого рода: y’=0, (x-1)^2=2, в результате получатся две точки: x1=1-sqrt2, x2=1+sqrt2. Отметьте полученные значения на области определения функции (рис. 1).
Определите знак производной на каждом из интервалов. На основе правила чередования знаков от «+» к «-» и от «-» к «+», получите, что точка максимума функции x1=1-sqrt2, а точка минимума x2=1+sqrt2. Этот же вывод можно сделать и по знаку второй производной.
Найдите критические точки первого рода: y’=0, (x-1)^2=2, в результате получатся две точки: x1=1-sqrt2, x2=1+sqrt2. Отметьте полученные значения на области определения функции (рис. 1).
Определите знак производной на каждом из интервалов. На основе правила чередования знаков от «+» к «-» и от «-» к «+», получите, что точка максимума функции x1=1-sqrt2, а точка минимума x2=1+sqrt2. Этот же вывод можно сделать и по знаку второй производной.