Как найти значение аргумента при заданном значении функции

Каждому значению функции соответствует одно или несколько значений аргумента, при которых выполняется заданная функциональная зависимость. Нахождение аргумента зависит от способа задания функции.

Инструкция

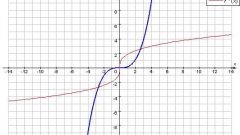
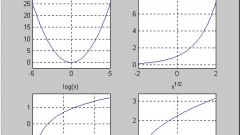
1. Функция может быть задана в виде математического выражения или графическим изображением. Если многочлен записан в каноническом виде, а график представляет узнаваемую кривую, то возможно определить значения аргумента на разных участках координатной плоскости. Например, если задана функция Y=√x, то аргумент может принимать только положительные значения. А для функции F=1/х недопустимо значение аргумента х=0.
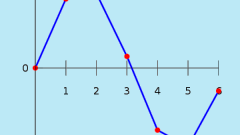
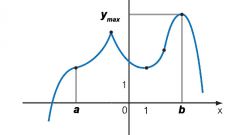
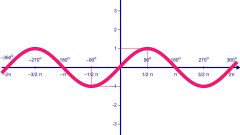
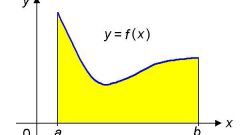
2. Если функция задана графически некоторой произвольной кривой, выводы о значениях аргумента можно делать лишь на видимой части графика в области координат. Возможно, что на разных интервалах действуют разные функциональные зависимости. Для нахождения значения аргумента, соответствующего определенному значению функции, найдите заданное число на оси OY. Проведите из этой точки перпендикуляр до пересечения с заданной кривой. Из полученной точки опустите перпендикуляр на ось ОХ. Число на оси ОХ является искомым значением аргумента. Возможно, что перпендикуляр оси ординат пересекает график в нескольких точках. В этом случае из каждой точки пересечения опустите перпендикуляры на ось абсцисс и запишите найденные числовые значения аргумента. Все они соответствуют заданному числовому значению функции.
3. Если функция задана математическим выражением, сначала упростите запись. Затем для нахождения аргумента решите уравнение, приравняв математическое выражение к заданному значению функции. Например, для функции Y=х² значению функции Y=4 соответствуют значения аргумента х₁=2 и х₂=-2. Эти значения получены из решения уравнения х² =4.