Как найти промежуточное значение

Для определения неизвестных промежуточных значений какой-либо функции или табличных данных в вычислительной математике используется аппарат интерполяции. Дискретный набор известных параметров может быть задан аргументами x0, х1 . . . xn и значениями функции yj=f(xj) (где j=0, 1, . . . , n). В простом частном случае задача поиска промежуточных значений указанного ряда может быть решена с помощью проведения линейной интерполяции.

Инструкция

1. Суть линейной интерполяции можно описать следующим допущением: в промежутке между известными соседними табличными значениями аргумента xi и xj рассматриваемую функцию y=f(x) можно приближенно считать линейной. Иными словами, на этом промежутке значение функции изменяется пропорционально изменению аргумента.
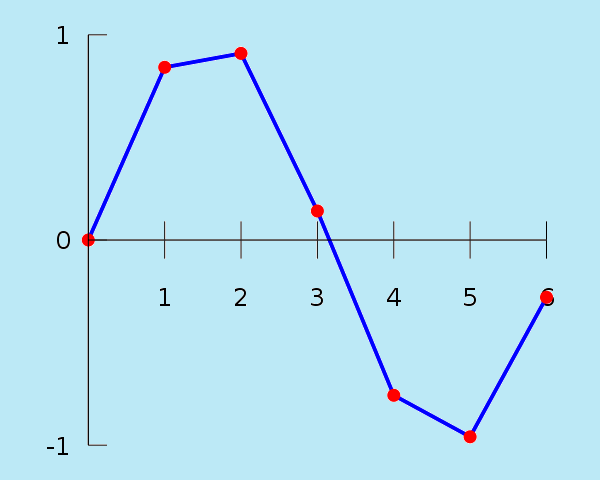
2. Более наглядно данное допущение можно отобразить в графическом виде в декартовой системе координат. Рассматриваемый отрезок функции уi и уj представляется непрерывной прямой с известными координатами. При поиске промежуточного значения функции Y, неизвестный аргумент Х находится между соседних значений хi и xj. Таким образом, можно записать следующие неравенства хi

   Выразите записанные условия в виде пропорции следующего вида: (yj – yi)/(хj – хi) = (Y – yi)/(Х – хi). Здесь yj и хj – конечные значения, yi, хi – начальные значения отрезка, Y и Х – искомые промежуточные значения.

   
   

   Как видно из пропорции при заданном приращении аргумента Х - хi легко найти соответствующее изменение функции Y – yi. Выразите приращение: Y – yi = ((yj – yi)/(хj – хi))*(Х – хi).

   
   

   Таким образом, промежуточные значения функции можно определить, зная лишь приращение, на которое произошло изменение аргумента. Вычислите разности yj – yi и хj – хi при заданном шаге аргумента Х – хi. Подставляя полученные значения в формулу приращения, найдите показатель изменения функции.

   
   

   Найдите промежуточное значение Y. Для этого к полученному значению приращения прибавьте начальный показатель функции уi на рассматриваемом отрезке. Аналогичным образом находится любое промежуточное значение с заданным шагом приращения.

   
   

   Если стоит задача в определении аргумента X по заданным значениям функции y=f(x), проводится обратная линейная интерполяция. Ее суть заключается в отыскании значения X с помощью той же пропорции, только теперь в качестве известного параметра выступает приращение функции Y – уi. С помощью аналогичных преобразований находится неизвестное промежуточное значение аргумента Х = ((yj – yi)/(хj – хi))/(Y – уi) + хi.
3. Выразите записанные условия в виде пропорции следующего вида: (yj – yi)/(хj – хi) = (Y – yi)/(Х – хi). Здесь yj и хj – конечные значения, yi, хi – начальные значения отрезка, Y и Х – искомые промежуточные значения.
4. Как видно из пропорции при заданном приращении аргумента Х - хi легко найти соответствующее изменение функции Y – yi. Выразите приращение: Y – yi = ((yj – yi)/(хj – хi))*(Х – хi).
5. Таким образом, промежуточные значения функции можно определить, зная лишь приращение, на которое произошло изменение аргумента. Вычислите разности yj – yi и хj – хi при заданном шаге аргумента Х – хi. Подставляя полученные значения в формулу приращения, найдите показатель изменения функции.
6. Найдите промежуточное значение Y. Для этого к полученному значению приращения прибавьте начальный показатель функции уi на рассматриваемом отрезке. Аналогичным образом находится любое промежуточное значение с заданным шагом приращения.
7. Если стоит задача в определении аргумента X по заданным значениям функции y=f(x), проводится обратная линейная интерполяция. Ее суть заключается в отыскании значения X с помощью той же пропорции, только теперь в качестве известного параметра выступает приращение функции Y – уi. С помощью аналогичных преобразований находится неизвестное промежуточное значение аргумента Х = ((yj – yi)/(хj – хi))/(Y – уi) + хi.