Инструкция
1
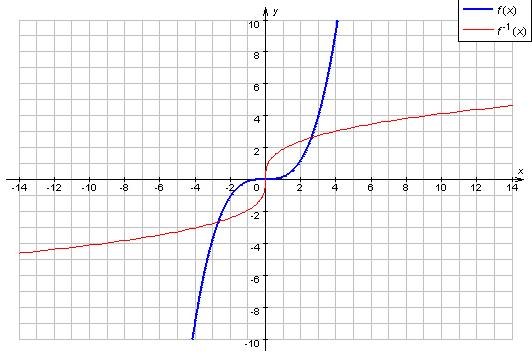
В общем случае при нахождении обратной функции для заданной у = f(x) выразите аргумент х через функцию у. Для этого воспользуйтесь правилами умножения обеих частей равенства на одно и то же значение, переносом многочленов выражений, при этом учитывайте смену знака. В простом случае рассмотрения показательных функций вида: y = (7/x) + 11, обращение аргумента х производится элементарно: 7/x = у-11, х = 7*(у-11). Искомая обратная функция имеет вид х = 7*(у-11).
2
Однако зачастую в функциях используются сложные степенные и логарифмические выражения, а также тригонометрические функции. В этом случае при нахождении обратной функции нужно учитывать известные свойства данных математических выражений.
3
Если в исходной функции аргумент х стоит под степенью, для получения обратной функции возьмите от данного выражения корень с тем же показателем. Например, для заданной функции у = 7+ х² обратная будет иметь вид: f(у) = √у -7.
4
При рассмотрении функции, где аргумент х представляет собой степень постоянного числа, примените определение логарифма. Из него следует, что для функции f(х) = ах обратной будет являться f(у) = logаy, причем основание логарифма а – в обоих случаях число, отличное от нуля. Так же и наоборот, рассматривая исходную логарифмическую функцию f(х) = logах, ее обратная функция представляет собой степенное выражение: f(у) = ау.
5
В частном случае исследования функции, содержащей натуральный логарифм ln х или десятичный lg х, т.е. логарифмы по основанию числа е и 10 соответственно, получение обратной функции проводится аналогично, только вместо основания а подставляется экспоненциальное число либо число 10. Например, f(х) = lg х -> f(у) = 10у и f(х) = ln х -> f(у) = еу.
6
Для тригонометрических функций обратными друг к другу являются следующие пары:
- y = cos x -> x = аrccos y;
- y = sin x -> x = аrcsin y;
- y = tan x -> x = аrctan y.
- y = cos x -> x = аrccos y;
- y = sin x -> x = аrcsin y;
- y = tan x -> x = аrctan y.
Обратите внимание
Следует помнить, что непрерывную функцию можно обратить лишь на тех промежутках ее значений, где она монотонна.