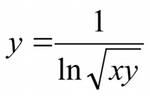Инструкция
1
«Функция» в математике – это понятие, которое отражает отношения элементов множеств между собой. Иначе говоря, это определенный закон, согласно которому каждому элементу одного множества ставится в соответствие элемент другого. При этом первое множество называется областью определения, а второе – областью значений. Такое определение «функции» называется интуитивным, близкие по смыслу значения – это «отображение», «операция».
2
Есть также теоретико-множественное определение, которое является более научным и более строгим. Согласно ему «функция» - это множество упорядоченных пар элементов вида (x, y), в котором x – элемент множества X, а y – множества Y. Новое множество удовлетворяет условию: для любого x существует такой единственный элемент y, что пара этих элементов – элемент нового множества. Объединение двух множеств по такому закону называется «бинарным отношением».
3
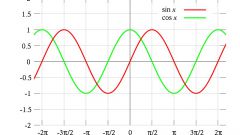
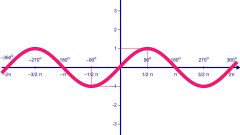
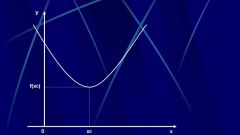
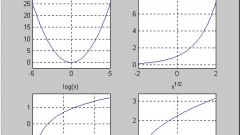
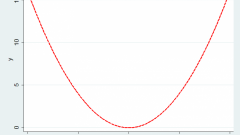
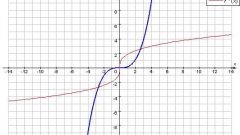
Математические функции используются в тригонометрии, в дифференциальном исчисления, нахождении производных и пределов, взятии интегралов, первообразных. Особенно эффективны функции при представлении бесконечных множеств, для этого используется графическое представление – построение графиков. График функции - это ее графическое построение из множества значений, где ось абсцисс - это значения аргумента x, а ось ординат - значения функции при этом значении аргумента f(x).
4
На графиках функций четко видны основные свойства поведения:
- возрастание: x > y => f(x) ≥ f(y);
- убывание: x f(x) ≤ f(y);
- монотонность (строгое возрастание x > y => f(x) > f(y) и убывание x f(x)
Известно, что математика, наука более точная, дает четкую запись свойств реальных объектов, в том числе в физике. Например, если задать в виде функции движение точки (положение точки в каждый момент времени), то вычисление производной этой функции в каждый момент времени даст функцию изменения скорости движения точки, а второй производной - функцию изменения ускорения. Также в физике используются тригонометрические, логарифмические, дифференциальные и прочие функции.

«Функция» в программировании – это часть кода программы, которая может вызываться из других частей (функций, процедур) столько, сколько это необходимо. При этом сама функция задается только один раз. Функция в данном случае – отдельная структура, на вход которой подаются определенные значения аргументов, а после окончания работы функции выдается результат. При этом как аргумент (аргументы), так и результат могут быть и действительным числом и числовым массивом.
5
Известно, что математика, наука более точная, дает четкую запись свойств реальных объектов, в том числе в физике. Например, если задать в виде функции движение точки (положение точки в каждый момент времени), то вычисление производной этой функции в каждый момент времени даст функцию изменения скорости движения точки, а второй производной - функцию изменения ускорения. Также в физике используются тригонометрические, логарифмические, дифференциальные и прочие функции.
6
«Функция» в программировании – это часть кода программы, которая может вызываться из других частей (функций, процедур) столько, сколько это необходимо. При этом сама функция задается только один раз. Функция в данном случае – отдельная структура, на вход которой подаются определенные значения аргументов, а после окончания работы функции выдается результат. При этом как аргумент (аргументы), так и результат могут быть и действительным числом и числовым массивом.