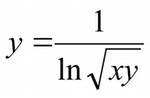Как находить область определения

Функцией называется соответствие, которое каждому числу x из некоторого заданного множества сопоставляет единственное число y. Множество значений x называется областью определения функции. Т.е. это множество всех допустимых значений аргумента (x), при которых функция y=f(x) определена (существует).

Инструкция

1. Если в функции присутствует дробь, и знаменатель содержит переменную (х), то знаменатель дроби не должен быть равен нулю, т.к. иначе такая дробь не может существовать. Чтобы найти область определения такой дроби, нужно весь знаменатель приравнять к нулю. Решив полученное уравнение, вы найдёте те значения переменной, которые необходимо исключить из области определения.
2. Если есть корень чётной степени, очевидно, что подкоренное выражение может быть только положительным числом. Далее, решаем неравенство, в котором подкоренное выражение меньше нуля. Полученные значения исключаем из области определения нашей функции.
3. Если есть логарифм. Область определения логарифма все числа, которые больше нуля. Т.е. чтобы найти значения переменной, не входящие в область определения, нужно составить и решить неравенство, в котором выражение под логарифмом меньше нуля.
4. Если в функции есть обратные тригонометрические функции, такие как арксинус и арккосинус. Они определены, только на промежутке [-1;1]. Следовательно, нужно проверить, при каких значениях переменной выражение, стоящее под этими функциями, попадает в этот промежуток.
5. В функции могут присутствовать сразу несколько из перечисленных вариантов, в этом случае необходимо рассмотреть их все и областью определения функции будет комбинация из всех результатов.