Инструкция
1
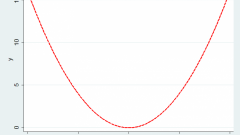
Определите, есть ли у задачи физический смысл. Так, если задача определения площади сводится к квадратному уравнению, то очевидно, что отрицательной площади быть не может: область допустимых значений [0; бесконечность). Если вы при решении получили пару корней -3, 3, то очевидно, что -3 в ОДЗ не попадает.
2
Решите, нужны ли вам комплексные значения. Использование таковых позволяет убрать ограничения со значений тригонометрических функций, чисел «под корнем» и ряда других ситуаций. Школьникам данный пункт можно смело игнорировать, т.к. даже ЕГЭ наличие комплексных чисел игнорирует.
3
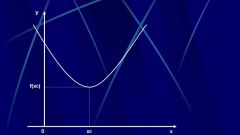
Рассмотрите ваше выражение и определите «состояние» искомых переменных. Являются ли они аргументами какой-либо функции(sin(x))? Находятся они в числителе или знаменателе? Возведены в целую, дробную или отрицательную степень? Учитывайте при этом все переменные (очевидно, что х может встречаться в нескольких местах уравнения).
4
Вспомните, какие ограничения каждая функция накладывает на переменную. Например: известно, что знаменатель в общем случае не может равняться нулю. Поэтому если в нижней части дроби образуется функция x-2, то из ОДЗ выпадает х=2, т.к. при этом нарушается смысл уравнения. Более простой пример: под корнем могут быть только положительные значения. Поэтому, если вам попадается конструкция «х под корнем», то можно смело ограничивать ОДЗ переменной х как [0, бесконечность).
5
Нарисуйте числовую ось и перенесите на нее все ограничения, наложенные примером. При этом «запретные» зоны заштриховывайте, отдельные точки выделяйте пустыми кружками. Как только все будет нанесено, «пустые» области прямой будут достоверно равняться ОДЗ: если решение уравнения попадает в отрезок без штриховки, то ответ допустим. Если таких зон не осталось, то приведенный пример не имеет решений.