Инструкция
1
Нaйти область определения – это первое, что следует делать при работе с функциями. Это множество чисел, которому принадлежит аргумент функции, с наложением некоторых ограничений, вытекающих из использования в ее выражении определенных математических конструкций, например, квадратного корня, дроби, логарифма и т.д.
2
Как правило, все эти структуры можно отнести к шести основных видам и их всевозможным комбинациям. Нужно решить одно или несколько неравенств, чтобы определить точки, в которых функция не может существовать.
3
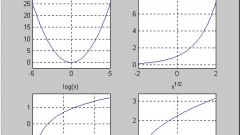
Степенная функция с показателем степени в виде дроби с четным знаменателемЭто функция вида u^(m/n). Очевидно, что подкоренное выражение не может быть отрицательным, следовательно, нужно решить неравенство u≥0.Пример 1: у=√(2•х - 10).Решение: составьте неравенство 2•х – 10 ≥ 0 → х ≥ 5. Область определения - интервал [5; +∞). При х
4
Логарифмическая функция вида log_a (u)В данном случае неравенство будет строгим u>0, поскольку выражение под знаком логарифма не может быть меньше нуля.Пример 2: у=log_3 (х - 9).Решение: х – 9 > 0 → х > 9 → (9; +∞).
5
Дробь вида u(х)/v(х)Очевидно, что знаменатель дроби не может обращаться в ноль, значит, критические точки можно найти из равенства v(х) = 0.Пример 3: у = 3•х² – 3/(х³ + 8).Решение: х³ + 8 = 0 → х³ = -8 → х=-2 → (-∞; -2)U(-2; +∞).
6
Тригонометрические функции tg u и ctg uНайдите ограничения из неравенства вида х ≠ π/2 + π•k.Пример 4: у = tg (х/2).Решение: х/2 ≠ π/2 + π•k → х ≠ π•(1 + 2•k).
7
Тригонометрические функции arcsin u и arcсos uРешите двустороннее неравенство -1 ≤ u ≤ 1.Пример 5: у = arcsin 4•х.Решение: -1 ≤ 4•х ≤ 1 → -1/4 ≤ х ≤ 1/4.
8
Показательно-степенные функции вида u(х)^v(х)Область определения имеет ограничение в виде u>0.Пример 6: у = (х³ + 125)^sinх.Решение: х³ + 125 >0 → х > -5 → (-5; +∞).
9
Присутствие в функции сразу двух или более из приведенных выражений предполагает наложение более строгих ограничений, учитывающих все составляющие. Находить их нужно по отдельности, а затем объединить в один интервал.