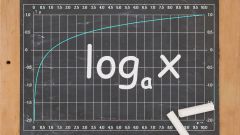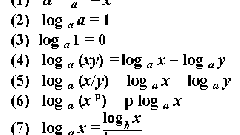Инструкция
1
Первым этапом нахождения области определения выражения можно сделать исключение деления на ноль. Если в выражении присутствует знаменатель, который может обратиться в ноль, следует найти все значения, при которых он обращается в ноль, и исключить их.Пример: 1/x. Знаменатель обращается в ноль при x = 0. 0 не будет входить в область определения выражения.(x-2)/((x^2)-3x+2). Знаменатель обращается в ноль при x = 1 и x = 2. Эти значения не будут входить в область определения выражения.
2
В выражении могут входить также различные иррациональности. Если в выражения входят корни четных степеней, то подкоренные выражения должны быть неотрицательны.Примеры: 2+v(x-4). Отсюда, x?4 - область определения данного выражения. x^(1/4) - корень четвертой степени из x. Следовательно, x?0 - область определения данного выражения.
3
В выражениях, в которых присутствуют логарифмы, необходимо помнить, что основание логарифма a определено при a>0 за исключением a=1. Выражение под знаком логарифма должно быть больше нуля.
4
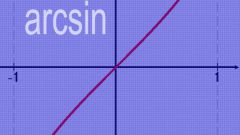
Если в выражении присутствуют функции арксинуса или арккосинуса, то область значений выражения, находящегося под знаком данной функции должна ограничиваться -1 слева и 1 справа. Отсюда и нужно находить область определения этого выражения.
5
В выражении могут фигурировать как деление, так и, например, квадратный корень. При нахождении области определения всего выражения необходимо учесть все моменты, которые могут привести к ограничению этой области. Исключив все неподходящие значения, нужно записать область определения. Область определения может принимать и любые действительные значения при отсутствии специфических точек.