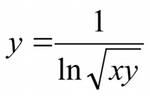Инструкция
1
Вспомните определение области определения функции и ее множества значений. Область определения функции – это фактически множество всех значений аргумента функции (или аргументов, если это функция от нескольких переменных), при которых она существует. Множество значений же – это множество возможных значений самой функции («игреков»).
2
Внимательно всмотритесь в вид функциональной зависимости, отраженной в вашей функции. Обратите внимание на то, какие математические ограничения наложены на независимую переменную вашей функции. Аргумент может быть под корнем, и это значит, что он должен быть только положительным; он может быть под знаком логарифма, что тоже указывает на его положительность, или, например, он может быть в знаменателе какой-нибудь дроби, тогда можно заключить, что он не должен быть равен нулю.
3
Выпишите отдельно выражение (равенство или неравенство), отражающее ограничения, наложенные на аргумент вашей функции. Например, «икс» не равен нулю или больше нуля. Это выражение может включать целый многочлен некоторой степени, содержащий переменную функции, или представлять собой некоторое трансцендентное соотношение. Решив записанное уравнение или неравенство, вы найдете те значения, которые позволительно принимать «иксу», то есть область определения.
4
Подставьте краевые возможные значения аргумента в вашу функцию, чтобы найти, какое множество значений функции соответствует множеству возможных значений ее аргумента. К примеру, если аргумент должен быть больше либо равен нулю, то вам необходимо подставить нулевое значение, а также понять, как (в какую сторону – положительную или отрицательную) будет меняться значение функции при нарастании или убывании ее переменной. Те значения, которые получаются при смене аргумента в области ее определения, и будут составлять множество значений функции.