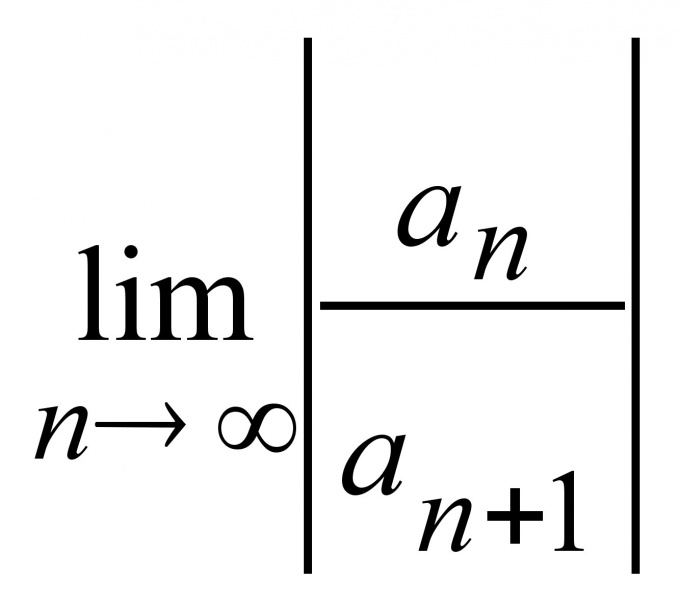Инструкция
1
Пусть задан числовой ряд U0 + U1 + U2 + U3 + … + Un + … = ∑Un. Un — выражение для общего члена этого ряда.
Суммируя члены ряда от начала до некоторого конечного n, вы получаете промежуточные суммы ряда.
Если по мере возрастания n эти суммы стремятся к какой-то конечной величине, то ряд называют сходящимся. Если же они возрастают или убывают бесконечно, то ряд расходится.
Суммируя члены ряда от начала до некоторого конечного n, вы получаете промежуточные суммы ряда.
Если по мере возрастания n эти суммы стремятся к какой-то конечной величине, то ряд называют сходящимся. Если же они возрастают или убывают бесконечно, то ряд расходится.
2
Чтобы определить, сходится ли заданный ряд, прежде всего проверьте, стремится ли его общий член Un к нулю при бесконечном возрастании n. Если этот предел не равен нулю, то ряд расходится. Если же равен, то ряд, возможно, сходящийся.Например, ряд степеней двойки: 1 + 2 + 4 + 8 + 16 + … + 2^n + … — расходящийся, поскольку его общий член в пределе стремится к бесконечности.Гармонический ряд 1 + 1/2 + 1/3 + 1/4 + … + 1/n + … расходится, хотя его общий член и стремится в пределе к нулю. С другой стороны, ряд 1 + 1/2 + 1/4 + 1/8 + … + 1/(2^n) + … сходится, и предел его суммы равен 2.
3
Предположим, что нам даны два ряда, общие члены которых равны соответственно Un и Vn. Если есть такое конечное N, что начиная с него, Un ≥ Vn, то эти ряды можно сравнивать между собой. Если нам известно, что ряд U сходится, то ряд V тоже совершенно точно сходится. Если же известно, что ряд V расходится, то и ряд U — расходящийся.
4
Если все члены ряда положительны, то его сходимость можно оценить по признаку Даламбера. Найдите коэффициент p = lim(U(n+1)/Un) при n → ∞. Если p < 1, то ряд сходится. При p > 1 ряд однозначно расходится, но если p = 1, то требуется дополнительное исследование.
5
Если знаки членов ряда чередуются, то есть ряд имеет вид U0 - U1 + U2 - … + ((-1)^n)Un + …, то такой ряд называется знакопеременным или знакочередующимся. Сходимость этого ряда определяется признаком Лейбница. Если общий член Un при возрастании n стремится к нулю, и для каждого n Un > U(n + 1), то ряд сходится.
6
При анализе функций чаще всего приходится иметь дело со степенными рядами. Степенной ряд — это функция, заданная выражением:f(x) = a0 + a1*x + a2*x^2 + a3*x^3 + … + an*x^n + …Сходимость такого ряда, естественно зависит от значения x. Поэтому для степенного ряда существует понятие диапазона всех возможных значений x, при которых ряд сходится. Этот диапазон равен (-R; R), где R — радиус сходимости. Внутри него ряд сходится всегда, за его пределами всегда расходится, на самой границе может как сходиться, так и расходиться.R = lim |an/a(n+1)| при n → ∞.Таким образом, для анализа сходимости степенного ряда достаточно найти R и проверить сходимость ряда на границе диапазона, то есть при x = ±R.
7
Например, пусть вам дан ряд, представляющий собой разложение в ряд Маклорена функции e^x:e^x = 1 + x + (x^2)/2! + (x^3)/3! + … + (x^n)/n! + …Отношение an/a(n+1) равно (1/n!)/(1/(n+1)!) = (n+1)!/n! = n + 1. Предел этого отношения при n → ∞ равен ∞. Следовательно, R = ∞, и ряд сходится на всей действительной оси.
Источники:
- Степенные ряды. Радиус сходимости