Инструкция
1
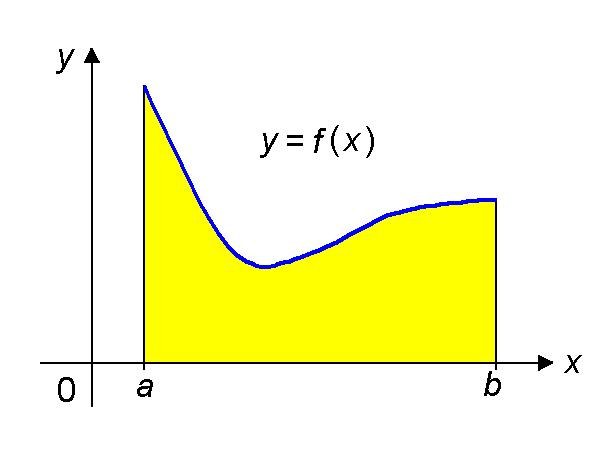
Доказательство непрерывности функции в точке осуществляется с помощью так называемых ε-Δ-рассуждений. ε-Δ определение звучит так: пусть x_0 принадлежит множеству X, тогда функция f(x) непрерывна в точке x_0, если для любого ε > 0 существует такое Δ > 0, что из |x - x_0|
Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.

Доказательство

По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|
Решите квадратное уравнение (x – x_0)^2 + 2*x_0*(x – x_0) – ε = 0. Найдите дискриминант D = √(4*x_0^2 + 4* ε) = 2*√(|x_0|^2 + ε). Тогда корень равен |x – x_0| = (-2*x_0 + 2*√(|x_0|^2 + ε))/2 = √(|x_0|^2 + ε). Итак, функция f(x) = x^2 непрерывна при |x – x_0| = √(|x_0|^2 + ε) = Δ.

Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):

f(x) = C (константа); все тригонометрические функции - sin x, cos x, tg x, ctg x и пр.

Пример 2: докажите непрерывность функции f(x) = sin x.

Доказательство

По определению непрерывности функции по ее бесконечно малому приращению запишите:

Δf = sin (x + Δx) - sin x.

Преобразуйте по формуле для тригонометрических функций:

Δf = 2*cos((x + Δx)/2)*sin(Δx/2).

Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.

2
Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.

Доказательство

По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|
Решите квадратное уравнение (x – x_0)^2 + 2*x_0*(x – x_0) – ε = 0. Найдите дискриминант D = √(4*x_0^2 + 4* ε) = 2*√(|x_0|^2 + ε). Тогда корень равен |x – x_0| = (-2*x_0 + 2*√(|x_0|^2 + ε))/2 = √(|x_0|^2 + ε). Итак, функция f(x) = x^2 непрерывна при |x – x_0| = √(|x_0|^2 + ε) = Δ.

Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):

f(x) = C (константа); все тригонометрические функции - sin x, cos x, tg x, ctg x и пр.

Пример 2: докажите непрерывность функции f(x) = sin x.

Доказательство

По определению непрерывности функции по ее бесконечно малому приращению запишите:

Δf = sin (x + Δx) - sin x.

Преобразуйте по формуле для тригонометрических функций:

Δf = 2*cos((x + Δx)/2)*sin(Δx/2).

Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
3
Решите квадратное уравнение (x – x_0)^2 + 2*x_0*(x – x_0) – ε = 0. Найдите дискриминант D = √(4*x_0^2 + 4* ε) = 2*√(|x_0|^2 + ε). Тогда корень равен |x – x_0| = (-2*x_0 + 2*√(|x_0|^2 + ε))/2 = √(|x_0|^2 + ε). Итак, функция f(x) = x^2 непрерывна при |x – x_0| = √(|x_0|^2 + ε) = Δ.
4
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):

f(x) = C (константа); все тригонометрические функции - sin x, cos x, tg x, ctg x и пр.
5
Пример 2: докажите непрерывность функции f(x) = sin x.

Доказательство

По определению непрерывности функции по ее бесконечно малому приращению запишите:

Δf = sin (x + Δx) - sin x.
6
Преобразуйте по формуле для тригонометрических функций:

Δf = 2*cos((x + Δx)/2)*sin(Δx/2).

Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.