Как найти икс нулевое

В качестве «икс нулевое» обозначается координата вершины параболы по оси абсцисс. В этой точке функция принимает наибольшее или наименьшее значение, поэтому x0 − точка экстремума функции.

Инструкция

1. Если имеется аналитическое задание функции, приведите ее к стандартному виду: A*x²+B*x+C=y(x), где A − старший коэффициент при x², B − средний коэффициент при x, C − свободный член. Обратите внимание, чтобы коэффициент при x² не равнялся нулю, иначе это будет уже не квадратичная функция.
2. Координата вершины параболы x0 по оси абсцисс находится по формуле: x0=-B/2A. В случае приведенного квадратного уравнения, то есть, когда A=1, формула упрощается: x0=-B/2. Если в уравнении нет «икса» в первой степени, значит, коэффициент B=0, и тогда x0 тоже обращается в нуль.
3. Чтобы найти координату вершины параболы по оси ординат, подставьте полученное значение для x0 в уравнение. Когда вы упростите выражение, с одной стороны у вас останется «игрек», с другой − некоторое число Q. Оно и показывает ординату вершины параболы: y0=Q.
4. Итак, исследование аналитически заданной функции дало вам точку на графике с координатами (x0;y0). Если старший коэффициент A > 0, то ветви параболы направлены вверх, и в вершине промежуток убывания будет сменяться промежутком возрастания. Если же A

   Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.

   
   

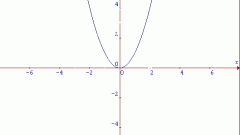
   Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.
5. Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.
6. Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.