Вам понадобится
- - линейка;
- - простой карандаш;
- - тетрадь;
- - ручка;
- - шаблон.
Инструкция
1
Найдите корни квадратного уравнения. Квадратное уравнение с одним неизвестным выглядит следующим образом: ax2+bx+c=0. Здесь х представляет собой искомое неизвестное; a, b и c являются известными коэффициентами, при этом a не должен быть равен 0. Если разделить обе части заданного квадратного уравнения на коэффициент a, то получите приведенное квадратное уравнение вида x2+px+q=0, в котором p=b/a и q=c/a. При условии, что один из коэффициентов b или c, либо оба равны нулю, полученное вами квадратное уравнение называется неполным.
2
Найдите дискриминант, который рассчитывается по формуле: b2-4ac. В том случае, если значение D больше 0, квадратное уравнение будет иметь два действительных корня; если D=0, найденные действительные корни будут равны между собой; если же D
3
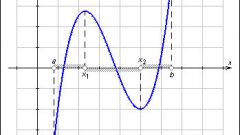
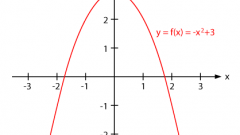
Графическим изображением квадратичной функции будет парабола. Определите дополнительные данные для построения графика этой квадратичной функции: направление «ветвей» параболы, ее вершину, а также уравнение оси симметрии. Если а>0, то «ветви» параболы устремлены будут вверх (в противном случае, «ветви» будут направлены вниз).
4
Для определения координат вершины параболы найдите х по формуле: -b/2а, после чего подставьте значение «икса» в квадратное уравнение для получения значения у.
5
И наконец, уравнение оси симметрии зависит от значения коэффициента c в исходном квадратном уравнении. К примеру, если заданное квадратное уравнение у=х2-6х+3, то ось симметрии будет проходить по линии, в которой х=3.
6
Зная направление «ветвей» параболы, координаты ее вершины, а также ось симметрии, постройте с помощью шаблона график заданного квадратного уравнения. Обозначьте на изображенном графике корни уравнения: они будут нулями функции.
Видео по теме
Полезный совет
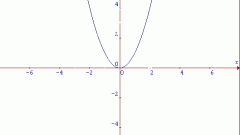
Для построения параболы-шаблона рассматривается канонический случай у=х2.
Источники:
- Графики и основные свойства элементарных функций
- как построить график функции с корнем