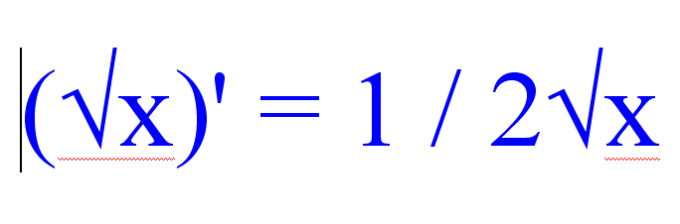Вам понадобится
- - карандаш;
- - бумага.
Инструкция
1
Перед тем как находить производную корня, обратите внимание на остальные функции, присутствующие в решаемом примере. Если в задаче имеется много подкоренных выражений, то воспользуйтесь следующим правилом нахождения производной квадратного корня:
(√х)' = 1 / 2√х.
(√х)' = 1 / 2√х.
2
А для нахождения производной кубического корня примените формулу:
(³√х)' = 1 / 3(³√х)²,
где через ³√х обозначен кубический корень из х.
(³√х)' = 1 / 3(³√х)²,
где через ³√х обозначен кубический корень из х.
3
Если в примере, предназначенном для дифференцирования, встречается переменная в дробных степенях, то переведите обозначение корня в степенную функцию с соответствующим показателем. Для квадратного корня это будет степень ½, а для кубического корня – ⅓:
√х = х ^ ½,
³√х = x ^ ⅓,
где символ ^ обозначает возведение в степень.
√х = х ^ ½,
³√х = x ^ ⅓,
где символ ^ обозначает возведение в степень.
4
Для нахождения производной степенной функции вообще и х^½, x^⅓, в частности, воспользуйтесь следующим правилом:
(х ^ n)' = n * x^(n-1).
Для производной корня из этого соотношения вытекает:
(х^½)' = ½ x ^ (-½) и
(x^⅓)' = ⅓ x ^ (-⅔).
(х ^ n)' = n * x^(n-1).
Для производной корня из этого соотношения вытекает:
(х^½)' = ½ x ^ (-½) и
(x^⅓)' = ⅓ x ^ (-⅔).
5
Продифференцировав все корни, внимательно посмотрите на остальные части примера. Если в ответе у вас получилось очень громоздкое выражение, то наверняка его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получилось небольшое число или компактное выражение.
6
Во многих задачах на нахождение производной, корни (квадратные и кубические) встречаются вместе с другими функциями. Чтобы найти производную корня в этом случае, применяйте следующие правила:
• производная константы (постоянного числа, C) равняется нулю: C' = 0;
• постоянный множитель выносится за знак производной: (k*f)' = k * (f)' (f – произвольная функция) ;
• производная суммы нескольких функций равняется сумме производных: (f + g)' = (f)' + (g)';
• производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)' = (f)'g + f (g)';
• производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)' = ((f)'g – f(g)') / g².
• производная константы (постоянного числа, C) равняется нулю: C' = 0;
• постоянный множитель выносится за знак производной: (k*f)' = k * (f)' (f – произвольная функция) ;
• производная суммы нескольких функций равняется сумме производных: (f + g)' = (f)' + (g)';
• производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)' = (f)'g + f (g)';
• производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)' = ((f)'g – f(g)') / g².
Обратите внимание
На этой странице вы сможете вычислять производную функции онлайн с получением подробного решения задачи. Решение производных функции производится с использованием тех правил дифференцирования, которые студенты изучают в курсе математического анализа в институте. Для того, чтобы найти производную функции нужно в поле "Функция" ввести функцию для дифференцирования согласно правил ввода данных.
Полезный совет
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.
Источники:
- производная корень из икс