Инструкция
1
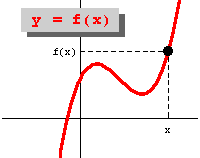
Исследовать область определения (допустимые значения аргумента x) и область значений (допустимые значения самой функции y(x)). Самые простые ограничения - это присутствие в выражении тригонометрические функций, корней или дроби с переменной в знаменателе.
2
Посмотреть, является ли функция чётной или нечётной (то есть проверить её симметричность относительно осей координат), либо периодической (в этом случае составные части графика будут повторяться).
3
Исследовать нули функции, то есть пересечения с осями координат: есть ли они, и если есть, то отметить характерные точки на заготовке графика, а также исследовать интервалы знакопостоянства.
4
Найти асимптоты графика функции, вертикальные и наклонные.

Для нахождения вертикальных асимптот исследуются точки разрыва слева и справа, для нахождения наклонных асимптот предел отдельно на плюс бесконечности и минус бесконечности отношения функции к х, то есть предел от f(x)/x. Если он конечен, то это коэффициент k из уравнения касательной (y =kx+b). Чтобы найти b, нужно найти предел на бесконечности в ту же сторону (то есть если k на плюс бесконечности, то и b на плюс бесконечности) от разности (f(x)-kx). Подставляем b в уравнение касательной. Если k или b найти не удалось, то есть предел равен бесконечности или не существует, то асимптот нет.
5
Найти первую производную от функции. Найти значения функции в полученных точках экстремума, указать области монотонного возрастания/убывания функции.

Если f'(x)>0 в каждой точке интервала (а,b), то функция f(x) возрастает на этом интервале.

Если f'(x)<0 в каждой точке интервала (a,b), то функция f(x) убывает на этом интервале.

Если производная при переходе через точку x0 меняет свой знак с плюса на минус, то x0 - точка максимума.

Если производная при переходе через точку x0 меняет свой знак с минуса на плюс, то x0 - точка минимума.
6
Найти вторую производную, то есть первую производную от первой производной.

Она покажет выпуклость/вогнутость и точки перегиба. Найти значения функции в точках перегиба.

Если f''(x)>0 в каждой точке интервала (а,b), то функция f(x) будет вогнутой на этом интервале.

Если f''(x)<0 в каждой точке интервала (а,b), то функция f(x) будет выпуклой на этом интервале.