Как найти координаты вершины параболы

График квадратичной функции называют параболой. Эта линия имеет весомое физическое значение. По параболам движутся некоторые небесные тела. Антенна в форме параболы фокусирует лучи, идущие параллельно оси симметрии параболы. Тела, брошенные вверх под углом, долетают до верхней точки и падают вниз, также описывая параболу. Очевидно, что всегда полезно знать координаты вершины этого движения.

Инструкция

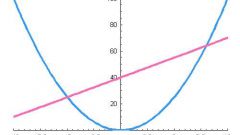
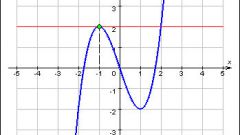
1. Квадратичная функция в общем виде записывается уравнением: y = ax² + bx + c. Графиком этого уравнения является парабола, ветви которой направлены вверх (при a > 0) или вниз (при a < 0). Школьникам предлагается просто запомнить формулу вычисления координат вершины параболы. Вершина параболы лежит в точке x0 = -b/2a. Подставив это значение в квадратное уравнение, получите y0: y0 = a(-b/2a)² - b²/2a + c = - b²/4a + c.
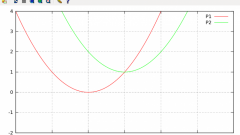
2. Людям, знакомым с понятием производной, легко найти вершину параболы. Независимо от положения ветвей параболы ее вершина является точкой экстремума (минимума, если ветви направлены вверх, или максимума, когда ветви направлены вниз). Чтобы найти точки предполагаемого экстремума любой функции, надо вычислить ее первую производную и приравнять ее к нулю. В общем виде производная квадратичной функции равна f'(x) = (ax² + bx + c)' = 2ax + b. Приравняв к нулю, вы получите 0 = 2ax0 + b => x0 = -b/2a.
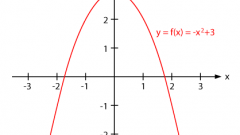
3. Парабола - симметричная линия. Ось симметрии проходит через вершину параболы. Зная точки пересечения параболы с осью координат X, можно легко найти абсциссу вершины x0. Пусть x1 и x2 - корни параболы (так называют точки пересечения параболы с осью абсцисс, поскольку эти значения обращают квадратное уравнение ax² + bx + c в ноль). При этом пусть |x2| > |x1|, тогда вершина параболы лежит посередине между ними и может быть найдена из следующего выражения: x0 = ½(|x2| - |x1|).