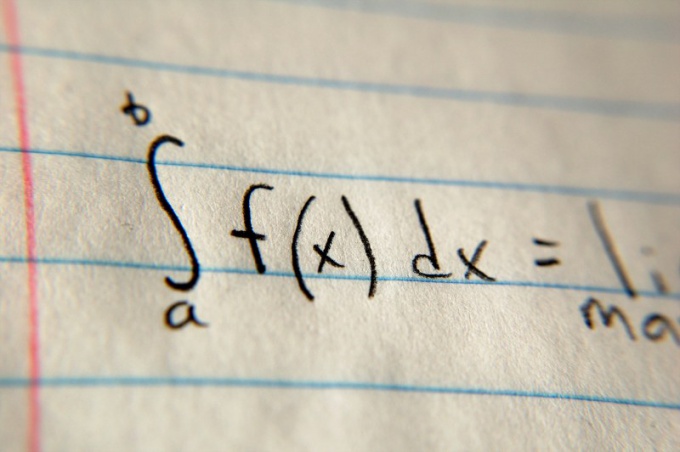Инструкция
1
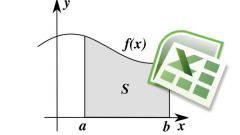
Чтобы вычислить площадь фигуры, ограниченной параболой, изобразите ее в декартовой системе координат. Для изображения параболы следует знать минимум три точки, одна должна быть вершиной. Чтобы найти координату вершины по оси X, подставьте известные данные в формулу x=-b/2a, по оси Y подставьте полученное значение аргумента в функцию. После этого проанализируйте данные графика, входящие в условие задачи. Если вершина ниже оси Х, то ветви будут направлены вверх, если выше — вниз. Остальные 2 точки — это координаты пересечения с осью ОХ. Заштрихуйте полученную фигуру. Это существенно облегчит решение данной задачи.
2
После этого определите пределы интегрирования. Обычно они указаны в условии задачи с помощью переменных a и b. Эти значения поместите в верней и нижней частях символа интеграла соответственно. После символа интеграла впишите значение функции в общем виде и помножьте его на dx (например, (x²)dx в случае с параболой). Затем вычислите первообразную значения функции в общем виде, воспользовавшись специальной таблицей по ссылке, приведенной в разделе «Дополнительные источники», после чего подставьте туда пределы интегрирования и найдите разность. Полученная разность и будет площадью.
3
Также существует возможность вычисления интеграла и программным методом. Для этого перейдите по ссылке, находящейся в разделе «Дополнительные источники», на специальный математический сайт. В открывшееся текстовое поле введите integral of f(x), где f(x) — запись функции, график которой ограничивает площадь фигуры на координатной плоскости. После ввода нажмите на кнопку в виде символа «равно». Открывшаяся страница изобразит полученную фигуру, а также покажет ход вычислений ее площади.