Как посчитать площадь фигуры

В задачах по геометрии часто требуется посчитать площадь плоской фигуры. В заданиях по стереометрии обычно вычисляют площадь граней. Найти площадь фигуры нередко нужно и в быту, например, при расчете количества необходимых стройматериалов. Для определения площади простейших фигур имеются специальные формулы. Однако, если фигура имеет сложную форму, то посчитать ее площадь иногда бывает не так-то просто.

Вам понадобится

• калькулятор или компьютер, линейка, рулетка, транспортир

Инструкция

1. Чтобы посчитать площадь простой фигуры, воспользуйтесь соответствующими математическими формулами:
   для расчета площади квадрата, возведите в вторую степень длину его стороны:
   
   Пкв = с²,
   
   где: Пкв – площадь квадрата, с – длина его стороны;
2. для нахождения площади прямоугольника, перемножьте длины его сторон:
   
   Ппр = д * ш,
   
   где: Ппр – площадь прямоугольника, д и ш – соответственно, его длина и ширина;
3. чтобы узнать площадь параллелограмма, умножьте длину любой из его сторон на длину высоты, опущенной на эту сторону.
   
   Если известны дины смежных сторон параллелограмма и угол между ними, то перемножьте длины этих сторон на синус угла между ними:
   
   Ппар = С1 * В1 = С2 * В2 = С1 * С2 * sinφ,
   
   где: Ппар - площадь параллелограмма
   
   С1 и С2 – длины сторон параллелограмма,
   
   В1 и В2 – соответственно, длины опущенных на них высот,
   
   φ – величина угла между смежными сторонами;
4. чтобы найти площадь ромба,
   
   умножьте длину стороны на длину высоты
   
   или
   
   умножьте квадрат стороны ромба на синус любого его угла
   
   или
   
   перемножьте длины его диагоналей и разделите полученное произведение на два:
   
   Промб = С * В = С² * sinφ = Д1 * Д2,
   
   где: Промб – площадь ромба, С – длина стороны, В – длина высоты, φ – величина угла между смежными сторонами, Д1 и Д2 – длины диагоналей ромба;
5. чтобы посчитать площадь треугольника,
   
   умножьте длину стороны на длину высоты и разделите полученное произведение на два,
   
   или
   
   умножьте половину произведения длин двух сторон на синус угла между ними,
   
   или
   
   умножьте полупериметр треугольника на радиус вписанной в треугольник окружности,
   
   или
   
   извлеките квадратный корень из произведения разностей полупериметра треугольника и каждой из его сторон (формула Герона):
   
   Птр = С * В / 2 = ½ * С1 * С2 * sinφ = п * р = √(п*(п-С1)*(п-С2)*(п-С3)),
   
   где: С и В – длина произвольной стороны и опущенной на нее высоты,
   
   С1, С2, С3 – длины сторон треугольника,
   
   φ – величина угла между сторонами (С1, С2),
   
   п – полупериметр треугольника: п = (С1+С2+С3)/2,
   
   р – радиус вписанной в треугольник окружности;
6. чтобы посчитать площадь трапеции, умножьте на высоту полусумму длин ее оснований:
   
   Птрап = (С1 + С2) / 2 * В,
   
   Птрап – площадь трапеции, С1 и С2 – длины оснований, а В – длина высоты трапеции;
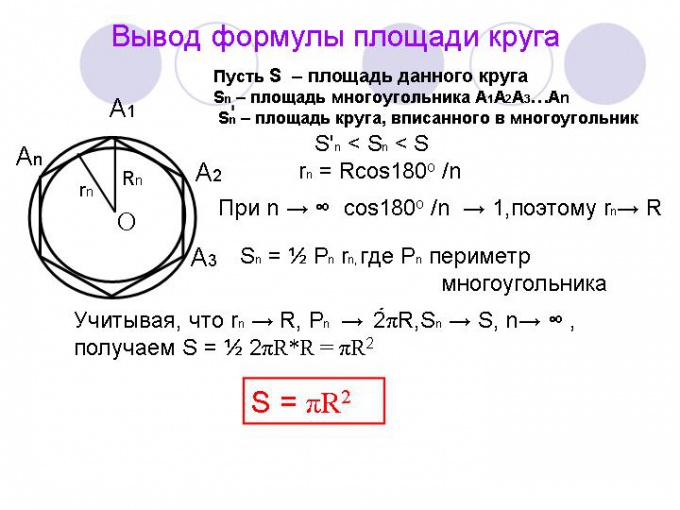
7. для расчета площади круга умножьте квадрат его радиуса на число «пи», примерно равное 3,14:
   
   Пкр = π * р²,
   
   где: р – радиус круга, π – число «пи» (3,14).
8. Для расчета площади более сложных фигур, разбейте их на несколько непересекающихся более простых фигур, найдите площадь каждой из них и сложите полученные результаты. Иногда площадь фигуры проще посчитать как разность площадей двух (или нескольких) простых фигур.