Вам понадобится
- Линейка, формулы нахождения площадей многоугольников
Инструкция
1
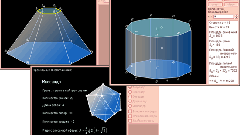
Чтобы рассчитать площадь поверхности призмы, найдите площадь одного из ее оснований. Используйте формулу в зависимости от того, какая это геометрическая фигура (многоугольник). Затем, найдите все стороны основания и, сложив их, получите его периметр. Умножив периметр на длину одного из боковых ребер (они равны), рассчитайте площадь боковой поверхности. Площадь поверхности призмы будет равна сумме площади боковой поверхности и удвоенной площади основания (поскольку их два) S=Sб+2•Sо.
2
Расчет площади поверхности произвольной пирамиды производится путем сложения площади основания, и каждой грани. Для правильной пирамиды (когда в ее основе лежит правильный многоугольник, а вершина проецируется на пересечение его диагоналей), можно использовать специальные формулы.
3
Найдите площадь и периметр основания правильной пирамиды. Рассчитайте площадь боковой поверхности, умножив половину периметра на апофему боковой грани (ее высоту) S= 0,5•P• a. Апофему найдите как высоту равнобедренного треугольника, которым является боковая грань правильной пирамиды. Сложите площадь основания и боковой поверхности и получите площадь полной поверхности.
4
Чтобы найти площадь полной поверхности кругового цилиндра, найдите сумму его радиуса и высоты, которая представляет собой отрезок соединяющий центры окружностей, которые являются основаниями цилиндра, а получившийся результат умножьте на радиус и число 6,28, S=6,28•r•(r+h).
5
Площадь поверхности кругового конуса найдите через радиус его основания и образующую. Для этого сумму радиуса и образующей (отрезка, соединяющего вершину конуса с произвольной точкой окружности основания), умножьте на радиус и число 3,14, . S=3,14•r•(r+l).
6
Для нахождения площади поверхности сферы найдите ее радиус. Тогда площадь будет равна произведению квадрата радиуса на число 12,56 S=12,56•r².