Инструкция
1
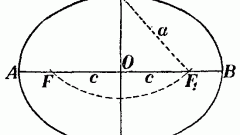
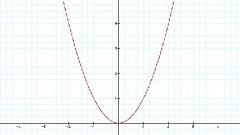
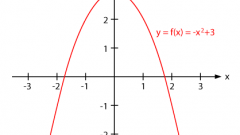
Приведите уравнение кривой к каноничному виду. Рассмотрите канонический вид уравнения для различных кривых второго порядка: парабола y²=2px; гипербола x²/q²-y²/h²=1; эллипс x²/q²+y²/h²=1; две пересекающиеся прямые x²/q²-y²/h²=0; точка x²/q²+y²/h²=0; две параллельные прямые x²/q²=1, одна прямая x²=0; мнимый эллипс x²/q²+y²/h²=-1.
2
Вычислите инварианты: Δ, D, S, B. Для кривой второго порядка Δ определяет, является ли кривая истинной - невырожденной или предельным случаем одной из истинных - вырожденной. D определяет симметрию кривой.
3
Определите, является ли кривая вырожденной. Вычислите Δ. Δ=afk-agg-bbk+bgc+cbg-cfc. Если Δ=0, то кривая вырожденная, если Δ не равен нулю, то невырожденная.
4
Выясните характер симметрии кривой. Вычислите D. D=a*f-b². Если он не равен нулю, то кривая имеет центр симметрии, если равен, то, соответственно, не имеет.
5
Вычислите S и B. S=a+f. Инвариант В равен сумме двух квадратных матриц: первая со столбцами a, c и c, k, вторая со столбцами f, g и g, k.
6
Определите тип кривой. Рассмотрите вырожденные кривые, когда Δ=0. Если D>0, то это точка. Если D
7
Рассмотрите невырожденные кривые - это эллипс, гипербола и парабола. Если D=0, то это парабола, ее уравнение y²=2px, где p>0. Если D0. Если D>0, а S0, h>0. Если D>0, а S>0, то это мнимый эллипс - нет ни одной точки на плоскости.
8
Выберите тип кривой второго порядка, который вам подходит. Приведите исходное уравнение, если требуется, к каноническому виду.
9
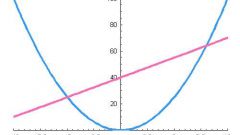
Рассмотрите для примера уравнение y²-6x=0. Получите коэффициенты, исходя из уравнения ax²+fy²+2bxy+2cx+2gy+k=0. Коэффициенты f=1, c=3, а остальные коэффициенты a, b, g, k равны нулю.
10
Вычислите величины Δ и D. Получите Δ=-3*1*3=-9, а D=0. Это значит, что кривая невырожденная, так как Δ не равен нулю. Поскольку D=0, то кривая не имеет центра симметрии. По совокупности признаков, уравнение является параболой. y²=6x.