Инструкция
1
Вспомним, что такое площадь.
Площадь — это мера плоской фигуры по отношению к стандартной фигуре. Или положительная величина, численное значение которой обладает следующими свойствами:

• Если фигуру можно разбить на части, которые будут являться простыми фигурами, то площадь такой фигуры будет равна сумме площадей ее частей

• Площадь квадрата со стороной, которая равна единице измерения, равна единице

• Равные фигуры обладают равными площадями
Из этих правил следует, что площадь это не конкретная величина, то есть площадь дает только условную характеристику какой-либо фигуре. Когда необходимо найти площадь произвольной фигуры, то нужно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить.
2
Пример:
Возьмем фигуру – прямоугольник, такой, в котором квадратный сантиметр укладывается в шесть раз. Тогда площадь такого прямоугольника будет равняться – 6 см2.
Если взять более сложную фигуру, например, трапецию, то получится что: Если трапеция такой величины, что квадратный сантиметр укладывается в нее только два раза, а третья часть не влезает целиком и остается небольшой треугольник. Чтобы измерить площадь этого оставшегося треугольника нужно применить к нему доли квадратного сантиметра, можно взять миллиметр. Правда, этот способ для сложных фигур не очень удобный. Поэтому для вычисления площади разных фигур существуют различные формулы. Если нужно вычислить площадь конкретной фигуры, то можно взять учебник по геометрии и вспомнить материал, который когда-то проходили в школе.
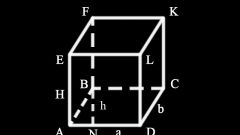
Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2