Инструкция
1
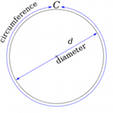
Используйте самую простую из формул вычисления площади поверхности шара (S), если известен его диаметр (D) или радиус (R). При этом придется использовать число Пи - математическую константу, показывающую неизменное отношение длины окружности к диаметру круга. Эта константа имеет бесконечное число знаков после десятичной запятой, поэтому вам придется определиться с необходимой точностью вычислений и округлить ее. Сделав это, умножьте число Пи на возведенный в квадрат диаметр шара - полученный результат и будет площадью сферы: S=π*D². Если известен не диаметр, а радиус, то в формулу надо добавить коэффициент, увеличивающий ее в четыре раза: S=4*π*R².
2
Если в условиях задачи сфера задана своими координатами в трехмерной декартовой системе, то начните расчет площади поверхности с нахождения ее радиуса. Для этого вам понадобятся координаты двух точек - являющейся центром шара (X₀,Y₀,Z₀) и любой из максимально удаленных от центра, то есть лежащих на поверхности сферы (X,Y,Z). Радиус сферы (R) будет равен квадратному корню из суммы квадратов попарных разностей координат по каждой из осей: R=√((X-X₀)²+(Y-Y₀)²+(Z-Z₀)²). Затем подставьте полученное значение в формулу из предыдущего шага. В общем виде она теперь будет выглядеть так: S = 4*π*(√((X-X₀)²+(Y-Y₀)²+(Z-Z₀)²))² = 4*π*((X-X₀)²+(Y-Y₀)²+(Z-Z₀)²).
3
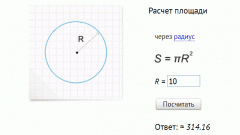
Если вам требуется, не вдаваясь в подробности вычислений, просто получить результат, то воспользуйтесь каким-либо из онлайн-калькуляторов. Например, тем, что размещен на странице http://board74.ru/articles/geometry/sphere.html. Перейдите на эту страницу и введите радиус шара в поле левее кнопки Calculate. Затем кликните кнопку и увидите результат расчета строкой ниже, рядом с формулой, использованной при вычислении. Здесь площадь поверхности сферы названа ее «боковой» поверхностью.
Видео по теме