Как найти площадь круга и его частей

Вычисление площади круга и его частей относится к задачам по геометрии 9-го класса. Умение их решать вам может потребоваться не только для того, чтобы помочь вашему ребенку с геометрией, но и для выполнения технических задач на работе или в быту. Применяя формулу вычисления площади круга, можно, например, рассчитать расход материалов по чертежам при строительстве круглого бассейна или вычислить площадь сечения электрического кабеля при выполнении электромонтажных работ.

Вам понадобится

• Для нахождения площади круга:
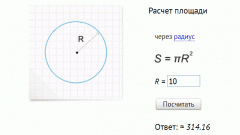
• - геометрическая формула нахождения площади круга S = Пхr2, где:
• - S - площадь круга;
• - П - число «пи», оно постоянно и равно значению 3,14;
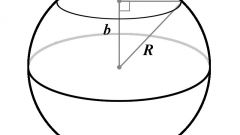
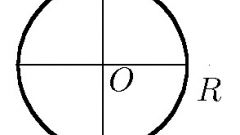
• - r - радиус круга.
• Для нахождения площади сектора круга:
• - геометрическая формула S=П х r2 / 360° х n°, где:
• - S - площадь сектора круга;
• - П - число «пи», оно постоянно и равно значению 3,14;
• - r - радиус круга;
• - n - значение центрального угла сектора в градусах.

Инструкция

1. Измерьте радиус окружности с помощью линейки. Вычислите значение площади круга по геометрической формуле нахождения площади круга (площадь круга равна произведению числа «пи» и квадрата радиуса круга).
2. Возведите для нахождения площади круга значение длины радиуса круга в квадрат, умножьте полученное число на число «пи» (его значение постоянно и равно 3,14). Так, воспользовавшись формулой, вы найдете площадь круга.
3. Измерьте угол сектора в градусах с помощью транспортира. Площадь круга вы уже знаете. Вычислите значение площади сектора круга по геометрической формуле (площадь сектора круга равна произведению площади круга с радиусом r на отношение угла сектора n° к углу полной окружности, т.е. 360°).
4. Поделите значение площади круга на 360 и умножьте на величину угла сектора в градусах. Так вы найдете величину площади сектора круга по градусной мере его угла.