Инструкция
1
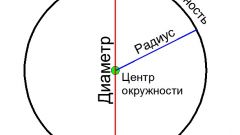
Пусть дан круг. Если радиус этого круга нам не известен, то можно выяснить его несколькими способами:
- узнать радиус простым измерением радиуса её окружности,
- если известна длина окружности этого круга, то её радиус можно вычислить по формуле R = L/2П, где L – длина окружности,
- можно описать квадрат около окружности, тогда её радиус будет равен половине стороны этого квадрата.
- узнать радиус простым измерением радиуса её окружности,
- если известна длина окружности этого круга, то её радиус можно вычислить по формуле R = L/2П, где L – длина окружности,
- можно описать квадрат около окружности, тогда её радиус будет равен половине стороны этого квадрата.
2
Из школьного курса геометрии известна теорема - площадь круга равна половине произведения длины ограничивающей ее окружности на радиус.
S = П*R*R
S = П*R*R
Обратите внимание
Существует несколько альтернативных формул для вычисления площади круга, все они путём преобразований приводятся к общей формуле, но могут быть полезны в конкретных ситуациях.
Площадь круга вписанного в треугольник.
S = П*((p-a)*tg(A/2))², где p - полупериметр, a и A - сторона и противолежащий угол треугольника соответственно, (p-a)*tg(A/2) - радиус вписанной окружности
Площадь круга описанного около треугольника.
S = П * (a/(2*sin(A)))², где a и A - сторона и противолежащий угол треугольника соответственно, a/(2*sin(A)) - радиус описанной окружности.
Площадь круга вписанного в треугольник.
S = П*((p-a)*tg(A/2))², где p - полупериметр, a и A - сторона и противолежащий угол треугольника соответственно, (p-a)*tg(A/2) - радиус вписанной окружности
Площадь круга описанного около треугольника.
S = П * (a/(2*sin(A)))², где a и A - сторона и противолежащий угол треугольника соответственно, a/(2*sin(A)) - радиус описанной окружности.