Вам понадобится
  • Линейка, карандаш, ластик.
Инструкция
1
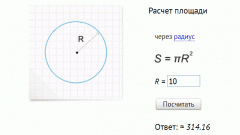
Шар является частным случаем простейшей объемной фигуры. Через него можно провести бесконечное количество сечений, и любое из них окажется кругом. Это произойдет независимо от того, насколько близко сечение расположено к центру шара. Вычислить площадь получившегося сечения проще всего в том случае, если оно проведено точно через центр шара, радиус которого известен. В таком случае площадь сечения равна:S=πR^2.
2
Другой фигурой, площадь сечения которой требуется найти в задачах по геометрии, является параллелепипед. Он имеет ребра и грани. Гранью называется одна из плоскостей параллелепипеда (куба), а ребром - сторона. Параллелепипед, у которого ребра и грани равны, называется кубом. Все сечения куба - квадраты. Зная это свойство, вычислите площадь сечения-квадрата:S=a^2, где a - ребро куба и сторона сечения.
3
Если в условиях задачи приведен обычный параллелепипед, у которого все грани являются разными, сечение может быть как квадратом, так и прямоугольником с различными сторонами. Сечение, проведенное параллельно двум квадратным граням, является квадратом, а сечение, проведенное параллельно двум прямоугольным - прямоугольником. Если сечение проходит через диагонали параллелепипеда, оно также является прямоугольником.
4
умножения диагонали нижнего основания на высоту параллелепипеда:S=d*h, где d - диагональ основания, h - высота основания.
5
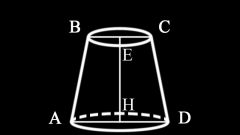
Конус - одна из тех фигур вращения, сечения которой могут иметь различную форму. Если рассечь конус параллельно нижнему основанию, сечением будет круг, а если провести сечение параллельно пополам через вершину конуса, получится треугольник. В других случаях сечениями будут трапециевидные фигуры.Если сечением является круг, вычисляйте его площадь по следующей формуле:S=πR^2.Площадь сечения, представляющего собой треугольник, равно произведению половины основания на высоту:S=1/2f*h , где f - основание треугольника, h - высота треугольника.