Инструкция
1
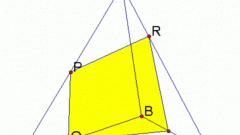
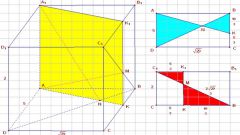
Выберите условия задачи так, чтобы они были исчерпывающими, но не избыточными. Секущую плоскость α следует задать общим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба вполне хватит координат любых трех его вершин. Возьмите, например, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.
2
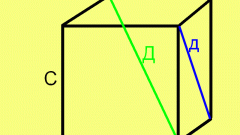
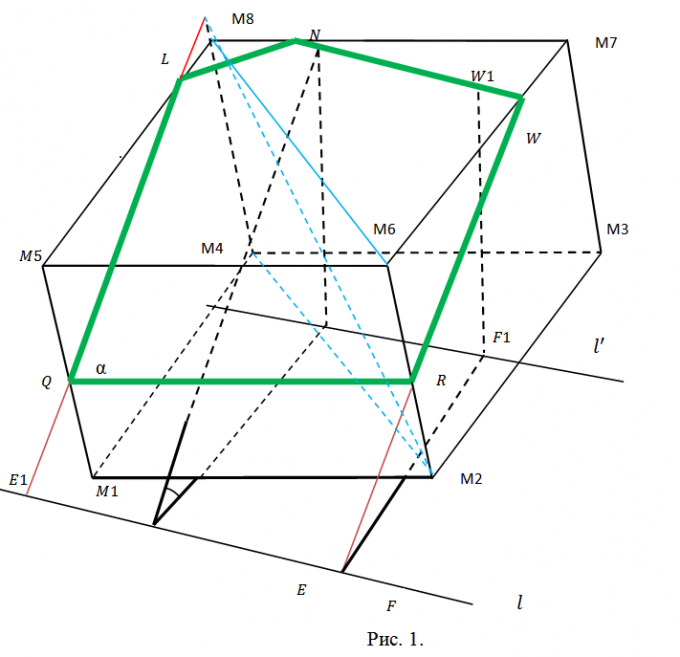
Определитесь с планом дальнейшей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью α. После этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади каждого из них с помощью свойств векторного произведения. Методика каждый раз одна и та же. Поэтому можно ограничиться точками Q и L и площадью треугольника ∆QLN.
3
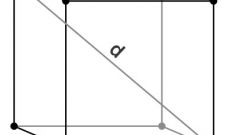
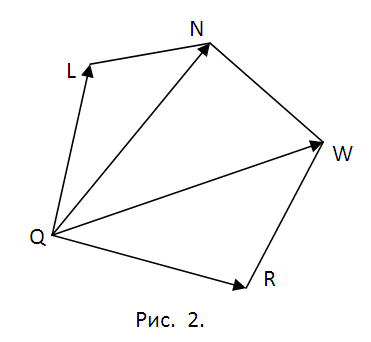
Направляющий вектор h прямой, содержащий ребро М1М5 (и точку Q), найдите как векторное произведение M1M2={x2-x1, y2-y1, z2-z1} и M2M3={x3-x2, y3-y2, z3-z2}, h={m1, n1, p1}=[M1M2× M2M3]. Полученный вектор является направляющим и для всех прочих боковых ребер. Длину ребра куба найдите как, например, ρ=√( (x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Если модуль вектора h |h|≠ρ, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)ρ. Теперь запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). После подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).
4
Очевидно, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. Затем повторите предыдущие рассуждения относительно точки L(lx, ly, lz) (см. рис. 4). Все дальнейшее, для N(nx, ny, nz) – точная копия это шага.
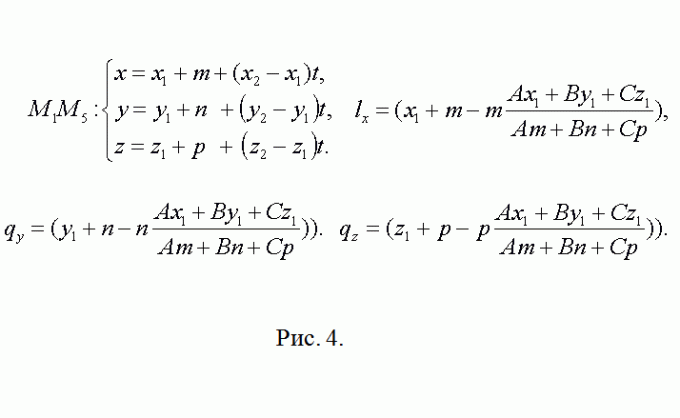
5
Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический смысл их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Поэтому площадь ∆QLN S1=(1/2)|[QL× QN]|. Следуйте предложенной методике и вычислите площади треугольников ∆QNW и ∆QWR - S1 и S2. Векторное произведение удобнее всего находить с помощью вектора-определителя (см. рис. 5). Запишите окончательный ответ S=S1+S2+S3.
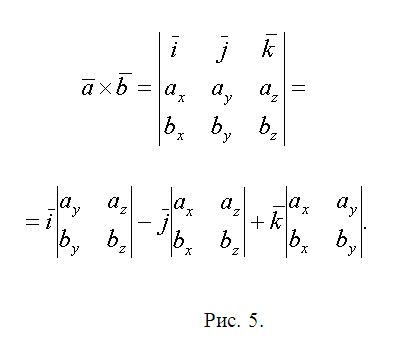
Источники:
- Шипачев В.С. Высшая математика. 3-е изд., стер. – М.: Высш. школа, 1996. 496 с.: ил.