Вам понадобится
  • - калькулятор;
  • - исходные данные.
Инструкция
1
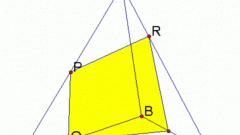
Чтобы найти площадь сечения параллелограмма, нужно знать значение его основания и высоту. Если, к примеру, известна лишь длина и ширина основания, то найдите диагональ, используя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).
2
Найдя значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный результат и будет величиной площадью поперечного сечения параллелограмма.
3
Если же сечение проходит вдоль двух оснований, то его площадь рассчитывайте по формуле: S=a*b.
4
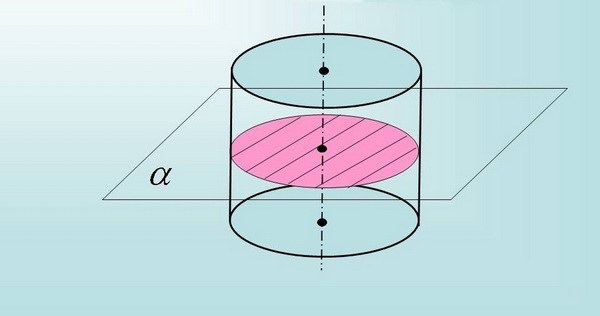
Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.
5
Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.
6
Самостоятельно вычислите неизвестную сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). После этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.
7
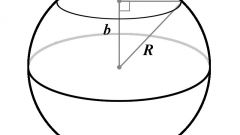
Площадь сечения шара определяется по формуле S = πR2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.