Инструкция
1
Если известна длина окружности (L), ее радиус (r) будет определяться отношением длины окружности к удвоенному числу Пи: r=L/(2∗π). Например, если известная длина окружности составляет пять метров, радиус можно определить так: 5/(2∗3,14) = 5/6,28 = 79,62 сантиметра.
2
Если известна площадь круга (S), радиус (r) можно определить как квадратный корень из соотношения площади и числа Пи: r=√(S/π). Например, если площадь круга составляет пять квадратных метров, радиус можно вычислить так: √(5/3,14) = √1,59 = 1,26 метра.
3
Если известны длины сторон (a и b) вписанного в круг прямоугольника, радиус окружности (r) будет определяться как половина диагонали этого прямоугольника. А поскольку длиной диагонали, согласно теореме Пифагора, можно считать квадратный корень из суммы длин сторон, возведенных в квадрат, радиус будет равен половине этой величины: r=0.5∗√(a² + b²). Например, если длины известных сторон равны двум и четырем метрам, длину радиуса можно определить так: 0.5∗√(2² + 4²) = 0.5∗√20 = 0.5∗4.47 = 2,24 метра.
4
Практические вычисления можно производить, например, в стандартном калькуляторе операционной системы Windows. Ссылка на его запуск помещена в один из подразделов главного меню на кнопке «Пуск». Раскрыв его, щелкните пункт «Все программы», затем пункт «Стандартные», потом пункт «Служебные» и наконец, пункт «Калькулятор». Альтернативный способ - воспользоваться диалогом запуска программ, который открывается нажатием сочетания клавиш WIN + R. В этом диалоге надо ввести команду calc и щелкнуть кнопку «OK».
Обратите внимание
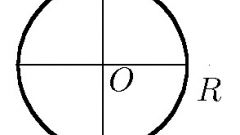
Как найти радиус окружности? Генон - удобный поиск ответов на вопросы. Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Круг — часть плоскости, ограниченная окружностью. Радиус — отрезок прямой, соединяющий центр окружности с какой-либо её точкой, а также длина этого отрезка.
Полезный совет
В зависимости от условия задачи радиус окружности вы можете найти так. Формула 1: R = Л / 2π, где Л – это длина окружности, а π – константа, равная 3,141 Формула 2: R = √( S / π), где S – это величина площади круга. Как найти радиус описанной окружности. Сначала давайте определимся с самим термином. Окружность называется описанной тогда, когда она касается всех вершин заданного многоугольника.