Вам понадобится
- Знать стороны многоугольника, его площадь/периметр.
Инструкция
1
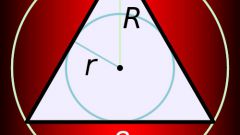
Подсчет радиуса описанной вокруг треугольника окружности.
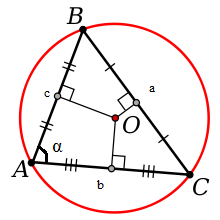
Если окружность описана вокруг треугольника со сторонами a, b, c, площадью S и углом ?, лежащим против стороны a, то ее радиус R может быть рассчитан по следующим формулам:
1) R = (a*b*c)/4S;
2) R = a/2sin?.
Если окружность описана вокруг треугольника со сторонами a, b, c, площадью S и углом ?, лежащим против стороны a, то ее радиус R может быть рассчитан по следующим формулам:
1) R = (a*b*c)/4S;
2) R = a/2sin?.
2
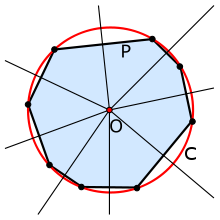
Подсчет радиуса окружности, описанной вокруг правильного многоугольника.
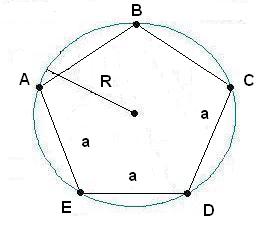
Для расчета радиуса окружности, описанной вокруг правильного многоугольника, нужно воспользоваться следующей формулой:
R = a/(2 x sin (360 / (2 x n))), где
a - сторона правильного многоугольника;
n - количество его сторон.
Для расчета радиуса окружности, описанной вокруг правильного многоугольника, нужно воспользоваться следующей формулой:
R = a/(2 x sin (360 / (2 x n))), где
a - сторона правильного многоугольника;
n - количество его сторон.
Обратите внимание
Вокруг многоугольника можно описать окружность только в том случае, если он правильный, т.е. все его стороны равны и все его углы равны.
Тезис, гласящий, что центром описанной вокруг многоугольника окружности является пересечение его серединных перпендикуляров, справедлив для всех правильных многоугольников.
Тезис, гласящий, что центром описанной вокруг многоугольника окружности является пересечение его серединных перпендикуляров, справедлив для всех правильных многоугольников.
Источники:
- как найти радиус многоугольника