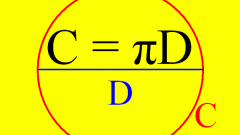Инструкция
1
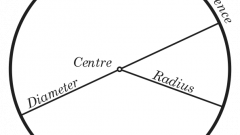
Чаще всего в задачах требуется вычислить длину окружности (L) по известному радиусу круга (R). Эти два параметра связаны между собой через самую, пожалуй, известную среди населения нашей планеты математическую константу - число Пи. Она и появилась в математике как выражение постоянного соотношения между длиной окружности и диаметром, то есть удвоенным радиусом. Поэтому для решения задачи умножайте радиус на два числа Пи: L = R*2*π.
2
Так как площадь круга (S) может быть выражена через его радиус, формулу из предыдущего шага можно трансформировать для вычисления периметра круга (L) по известной площади. Радиус равен квадратному корню из соотношения между площадью и числом Пи - подставьте это выражение в формулу из предыдущего шага. У вас должна получиться такая формула: L = √(S/π)*2*π. Ее можно немного упростить: L = 2*√(S*π).
3
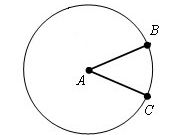
Длину окружности в целом можно рассчитать и зная длину какой-нибудь ее части (l) вместе с величиной сопоставленного этой дуге центрального угла (α). Соотношение двух исходных величин равно радиусу круга, если угол выражен в радианах. Подставьте это выражение радиуса в формулу из первого шага, и вы получите такое равенство: L = l/α*2*π.
4
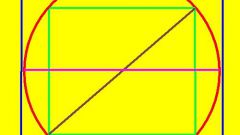
Если в исходных условиях приведена длина стороны квадрата (А), вписанного в окружность, одного этого значения будет достаточно для нахождения периметра круга. Радиус в этом случае будет равен произведению длины стороны четырехугольника на квадратный корень из двойки. Подставьте это выражение во все ту же формулу из первого шага, чтобы получить такое равенство: L = А*√2*2*π.
5
Зная ту же величину - длину стороны (А) - квадрата, описанного около окружности, можно получить еще более простую формулу расчета периметра круга (L). Так как в этом случае длина стороны будет совпадать с диаметром, используйте для вычисления такую формулу: L = А*π.